1. Pontszerű test
    1. Pontszerű test modellje
      • A pontszerű test a legegyszerűbb olyan modell, amellyel bizonyos esetekben a valóságos testek mozgását helyettesíteni lehet.
      • Ha valamely test mozgásának leírásakor a test kiterjedése nem játszik szerepet, akkor az adott test egy pontszerű modellel helyettesíthető.

      A pontszerű test olyan idealizált modell, amelynek kiterjedése nincs, de tömege van.

    2. Pontszerű test egyensúlya

      Pontszerű test akkor van egyensúlyban, ha a ráható erők vektori eredője nulla.

    3. Pontszerű test mozgása

      Különböző mozgások dinamikai feltétele Newton II. törvényéből levezethető.

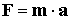
      1. Egyenes vonalú egyenletes mozgás

        Egyenes vonalú egyenletes mozgás dinamikai feltétele, hogy a testre ne hasson erő vagy a testre ható erők eredője nulla legyen.

      2. Egyenes vonalú egyenletesen változó mozgás

        Egyenes vonalú egyenletesen változó mozgás dinamikai feltétele, hogy a testre állandó nagyságú és irányú eredőerő hasson.

      3. Egyenletes körmozgás

        Egyenletes körmozgást akkor végez egy test, ha a ráható erők eredője állandó nagyságú, és iránya minden pillanatban a kör középpontja felé mutat.

      4. Egyenletesen változó körmozgás

        Pontszerű test egyenletesen változó körmozgásához olyan eredő erő szükséges, amely két komponensből áll:

        Érintő irányú erő:

        • a pálya menti sebességet változtatja
        • nagysága állandó
        • iránya mindig érintő irányú

        Centripetális erő

        • körpályán való maradáshoz szükséges erő
        • nagysága az idő négyzetével arányosan változik
        • iránya mindig sugár irányú

        Az eredő erőt Pitagorasz-tétel segítségével számoljuk ki.

        Fé = m ∙ aé = m ∙ r ∙ β = áll. (aé = r ∙ β)

        Fcp = m ∙ acp = m ∙ ωt2 ∙ r = m ∙ r ∙ β2 ∙ t2 változó
        (mert t változik!)

         
         

         

      5. Harmonikus rezgőmozgás

        Harmonikus rezgőmozgás létrejöttének dinamikai feltétele, hogy a testre olyan eredőerő hasson, ami a kitéréssel arányos, de vele ellentétes irányú.

  2. Pontrendszer
    1. A pontrendszer fogalma

      Egymással kölcsönhatásban lévő pontszerű testekből álló rendszert pontrendszernek nevezünk.
      Ilyen pl.:

      • két biliárdgolyó ütközése
      • egymással kapcsolatban lévő vasúti kocsik
      • Naprendszer tagjai, ha a forgástól eltekintünk

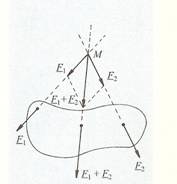
      A pontrendszer tagjaira hathatnak:

      • Külső erő (F1, F2)
      • Belső erők (F21, F12) a rendszer tagjai között működő erők.
      • A belső erők eredője Newton III. törvényéből adódóan mindig nulla.

       

    2. Pontrendszer mozgásának dinamikai leírása

      A pontrendszer mozgásának a leírásánál a következőkre van szükség:

      • A pontrendszer ismeretében meg kell határozni az egyes tagjaira ható erőket.
      • Az erők ismeretében fel kell írni a dinamika alapegyenletét a pontrendszer minden egyes tagjára. Ezek adják az egyes testek mozgásegyenleteit.
      • A rendszer tagjai közt fennálló kapcsolatok segítségével fel kell íni a kényszerfeltételeket.

      Kényszerfeltételek
      Pontrendszer tagjainak gyorsulásai közötti matematikai kapcsolatot kényszerfeltételnek nevezzük.

      • Az ábrán látható két kiskocsi a kötél nyújthatatlansága miatt együtt fog mozogni.
      • Ebből következik, hogy pillanatnyi sebességük és gyorsulásuk is mindig azonos.
      • Gondolatmenetünk során tehát azt mondhatjuk, hogy a két test gyorsulása azonos.
    3. Lendület és lendület-megmaradás pontrendszer esetén
      • Ha felírjuk a pontrendszer egyes tagjainak az impulzusát, és ezeket az impulzusokat, mint vektorokat összegezzük, akkor a pontrendszer összimpulzusát kapjuk.
      • A pontrendszer összimpulzusát a belső erők nem változtatják meg, mert azok eredője nulla.
      • Amennyiben egy pontrendszer tagjaira csak belső erők hatnak, a pontrendszer összimpulzusa állandó. Természetesen az egyes testek impulzusa megváltozhat a rájuk ható belső erők hatására.

      Lendülettélet pontrendszerre
      Egy pontrendszer lendületváltozása megegyezik a pontrendszerre ható külső erők eredőjének erőlökésével.

      Lendület-megmaradás pontrendszerre
      Ha egy pontrendszerre csak belső erők hatnak, akkor azt zárt rendszernek nevezzük. Zárt pontrendszer összimpulzusa állandó.

    4. Munkatétel pontrendszer esetén

      Pontrendszer mozgási energiájának a megváltozását nemcsak külső, de a belső erő munkája is előidézheti.
      Az ábra szerint a két kiskocsi között megfeszített rugó van. Így mindkét kiskocsira belső erő hat. Ha a cérnaszálat elégetjük a kocsik ellentétes irányban kezdik el a mozgásukat. A rugóban tárolt energia a kiskocsik mozgási energiájává alakul át. Így ebben az esetben a belső erők változtatták meg a pontrendszer mozgási energiáját.

      Egy pontrendszer mozgási energiájának megváltozása megegyezik a külső és a belső erők munkájának az összegével.

  3. Merev test
    1. A merev test modelljének jellemzése

      Az olyan testeket, amelyeknél a fizikai probléma leírása szempontjából nem elhanyagolható a mérete kiterjedt testeknek nevezzük.
      A kiterjedt testeknek két fajtájuk van:

      • Vannak olyan kiterjedt testek, amelyek nagy erő hatására sem változtatják az alakjukat. Az ilyen testeket merev testeknek nevezzük.
      • A kiterjedt testek másik csoportjának erő hatására megváltozik az alakja. Az ilyen testeket deformálható testeknek nevezzük.

      A merev test olyan elképzelt modell, amelynek mérete a fizikai jelenség leírása szempontjából nem elhanyagolható, és nagy erő hatására sem változtatja meg az ilyen test az alakját, méretét.

    2. Hatásvonal és támadáspont

      Jele: M

      Az erő támadáspontjának nevezzük azt a pontot, ahol az erőátvitel történik az egyik testről a másikra.

      Az erő hatásvonala az erő támadáspontján átmenő egyenes, amely mentén az erő hat. Egy erőt a hatásvonala mentén tetszőlegesen  
      eltolhatunk, és közben a hatása nem változik.

       

       

    3. Forgatónyomaték

      Az erő és az erőkar szorzatát forgatónyomatéknak nevezzük.
      Jele: M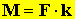

      Erőkar az erő hatásvonalának a forgástengelytől való távolsága.
      A forgatónyomaték vektormennyiség.
      Mértékegysége:
      A tengely körül az erő kétféle irányba forgathatja a testet.

      • Pozitívnak nevezzük az óramutató járásával ellentétes forgást.
      • Negatívnak nevezzük az óramutató járásával megegyező forgást.
    4. Merev test viselkedése egy erő hatására

      Egyetlen erő hatására a merev test az erő irányába gyorsul.

    5. Merev test viselkedése két erő hatására

      • Két erő hatására a merev test akkor van egyensúlyban, ha a két erő közös hatásvonalú, egyenlő nagyságú, de ellentétes irányú.
      • Ha a két erő egymással szöget zár be, akkor a merev test az eredőerő irányába gyorsul.
    6. Merev test viselkedése három egymással szöget bezáró erő hatására

      Három erő hatására akkor lesz a merev test egyensúlyban, ha

      • a három erő hatásvonala egy közös pontban metszi egymást és
      • bármely két erő eredőjével egyenlő nagyságú, közös hatásvonalú, de ellentétes irányú a harmadik erő.
    7. Párhuzamos hatásvonalú erők összegzése
      1. Egyezőirányú párhuzamos hatásvonalú erők összegzése

        Ha egy merev testre párhuzamos hatásvonalú egyezőirányú erők hatnak, akkor ezeknek az erőknek az eredőjét szerkesztéssel és számolással egyaránt meg tudjuk határozni.

        Szerkesztés

        • A merev testre ható két párhuzamos hatásvonalú erő az F1 és az F2.
        • Felveszünk két segéderőt (F' és -F') és ezek segítségével megszerkesztjük F1'-t és F2'-t.
        • Ez a két erő egymással már 180°-nál kisebb szöget zár be, így megszerkeszthető az eredőerő.
        • Szerkesztés után az eredőerőt visszacsúsztatjuk a hatásvonal mentén a testre.

        Párhuzamos hatásvonalú egyezőirányú erők eredőjének

        • hatásvonala párhuzamos az összetevő erők hatásvonalával, és azok között helyezkedik el
        • iránya megegyezik az összetevő erők irányával
        • nagysága megegyezik az összetevő erők nagyságának az összegével

        Számolás
        Párhuzamos hatásvonalú egyezőirányú erők eredőjének a hatásvonala az az egyenes, amelyre nézve az összetevőerők forgatónyomatékának az összege nulla.

      2. Ellentétes irányú párhuzamos hatásvonalú erők összegzése

        Az eredőerő szerkesztése az előzőekhez hasonlóan történik.

        Párhuzamos hatásvonalú ellentétes irányú erők eredőjének

        • hatásvonala párhuzamos az összetevő erők hatásvonalával, és az összetevők hatásvonalán kívül, a nagyobbik oldalán helyezkedik el
        • iránya megegyezik a nagyobb összetevő erő irányával
        • nagysága megegyezik az összetevő erők nagyságának a különbségével.

           
    8. Erőpár

      Erőpárnak nevezzük azt az erőrendszert, amely

      • Két párhuzamos hatásvonalú
      • Egyenlő nagyságú
      • Ellentétes irányú erőkből áll
      • Ilyen erőrendszer nem helyettesíthető egyetlen eredőerővel
      • Ez az erőrendszer forgatja a testet
      • Az erőpár forgatónyomatéka egyenlő az erő hatásvonalának a távolsága és az erő nagyságának a szorzatával
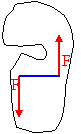
      Ha pl. bármely erő támadáspontjára felírjuk a forgatónyomatékot:
      , ahol d az erők hatásvonalainak távolsága.
      Erőpár forgatóhatását csak egy másik erőpárral lehet kiegyensúlyozni.
    9. Merev test egyensúlyának általános feltétele

      A merev test akkor lesz egyensúlyban, ha egyszerre két feltétel teljesül:

      • a testre ható erők eredője nulla. ΣF=0 (nem végez haladó mozgást a test)
      • a forgatónyomatékok vektori összege nulla. ΣM=0 (nem forog a test)
    10. Súlyvonal és súlypont

      Minden merev test részecskéjére hat nehézségi erő. Ezek azonos irányú párhuzamos hatásvonalú erők.
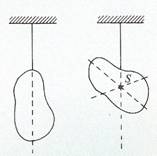
      A részecskékre ható nehézségi erők eredőerőjének hatásvonalát súlyvonalnak, támadáspontját súlypontnak nevezzük.

      Kísérletileg ezt úgy tudjuk meghatározni, hogy a merev testet egy pontjában felfüggesztjük.

      • A tartó erő hatásvonalába az egyik súlyvonal.
      • Ha több pontban felfüggesztjük a merev testet, akkor több súlyvonalat is megrajzolhatunk.
      • Súlypont a súlyvonalak metszéspontja, az a pont, amelyre nézve a merev test részecskéire ható nehézségi erők forgatónyomatékainak előjeles összege nulla. (Ha a merev testet alátámasztjuk, akkor egyensúlyi helyzetben van.)

         
    11. Egyensúlyi helyzetek

      Egy merev test addig van egyensúlyban, amíg a ráható erők és a forgatónyomatékok vektori összege nulla. A test mindaddig marad ebben az állapotban, ameddig valamilyen hatás ki nem mozdítja ebből az állapotból.

      Az egyensúlyi helyzetek azonban lényegesen különbözhetnek egymástól.

      Biztos vagy stabil az az egyensúlyi helyzet, amelyből ha kimozdítjuk a testet, majd magára hagyjuk, az visszatér az eredeti helyzetébe. A forgástengely a súlypont felett van.
      Bizonytalan vagy labilis az az egyensúlyi helyzet, amelyből, ha bármilyen kis mértékben kimozdítjuk a testet, majd magára hagyjuk, a test nem tér vissza eredeti helyzetébe, hanem a kimozdítás irányában továbbmozogva új egyensúlyi helyzetet foglal el. A forgástengely a súlypont alatt van.

      Közömbös vagy indifferens az az egyensúlyi helyzet, amelyből ha kimozdítjuk a testet, majd magára hagyjuk, a test a kimozdulás helyzetében marad egyensúlyban. A forgástengely egybeesik a súlyponttal.
    12. Egyszerű gépek

      Az egyszerű gépek olyan eszközök:

      • megváltoztatják az erő irányát
      • megsokszorozzák az általunk kifejtett erő.

      Az egyszerű gépek fajtái:

      • emelő típusú egyszerű gépek
      • lejtő típusú egyszerű gépek

      Emelő típusú egyszerű gépek

      Egyoldalú emelőnél a teher és az emelő erő az emelő ugyanazon oldalán van.

      Kétoldalú emelőnél az a teher és az emelő két különböző oldalon van.

      olló, mérleg

      Állócsiga

      • A csiga tengelye rögzített.
      • Látható, hogy csak az erő irányát változtatja meg.

      Mozgócsiga

      • A csiga tengelye nincs rögzítve.
      • Egyensúly esetén teljesül:

      Csigasor

      • A csigasornál az állócsigát mozgócsigával kombinálják. Így az erő nagyságát és az irányát is lehet változtatni.
      • Ha n darab álló és n db mozgócsiga van, akkor az egyensúlyozó erő:

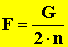
      A daru köteleit is ilyen összeállításon keresztül vezetik.

      Arkhimédeszi csigasor

      • Minden újabb mozgócsiga beiktatása felezi az erőt.
      • Ha a mozgócsigák száma n, akkor a tartóerő:

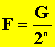
      10 mozgócsiga alkalmazásával 1 tonna tömegű terhet kevesebb, mint 1 kg tömeggel egyensúlyban tudunk tartani.

       

      -

      Két közös tengelyű, különböző sugarú csiga.

      Példák:

      • kerekeskút
      • bicikli kormánya
      • autók kormánya

      Lejtő típusú egyszerű gépek

      Lejtőn a test egyensúlyban tartásához kisebb erőre van szükség, mint a test súlya.

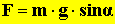
      • A kifejtet erő annál kisebb, minél kisebb a lejtő hajlásszöge.
      • Ezt az elvet használják a hegyi szerpentineknél is.

       

      Csavar

      		  

      Ék
      Egy henger oldalába vágott lejtő   Mozgatható lejtő
       
    13. Forgómozgás alaptörvénye

      A forgómozgást leíró dinamikai törvény

      A forgatónyomaték egyenesen arányos a szöggyorsulással, az arányossági tényező a tehetetlenségi nyomaték.

    14. Tehetetlenségi nyomaték

      Jele:
      A tehetetlenségi nyomaték értéke nemcsak a test tömegétől, hanem a tengelyhez viszonyított tömegeloszlástól függ.

      Bármely forgó test a forgástengelyhez viszonyított tehetetlenségi nyomatékát megkapjuk, ha az egyes tömegpontoknak forgástengelytől mért távolság négyzetét szorozzuk a tömegpont tömegével, majd ezeket összegezzük.

    15. Merev test síkmozgása

      Merev test síkmozgásáról akkor beszélünk, ha a merev test tengelye nincs rögzítve, így a forgómozgás mellett haladó mozgást is végez.

      A haladómozgást és a forgómozgást leíró törvényszerűségek alakra megegyeznek, és az egyenletekben szereplő mennyiségek megfelelnek egymásnak.

      HALADÓMOZGÁS FORGÓMOZGÁS
      megtett út s szögelfordulás
      sebesség szögsebesség
      gyorsulás   szöggyorsulás
      tömeg m tehetetlenségi nyomaték
      erő F forgatónyomaték M
      dinamika alapegyenletes forgómozgás alapegyenlete
      impulzus perdület
      impulzustétel perdülettétel

      Ha a merev test tisztán gördül, akkor

      • a kerületi sebesség megegyezik a tömegközéppont sebességével.