• A körmozgás az időben ismétlődő periodikus mozgások közé tartozik.
• A mozgás pályája egy kör.
• A mozgás egy periódusa az a pályaszakasz, amelyet a test akkor fut be, ha a körkerület egy pontjából elindul, megtesz egy teljes körívet, és visszatér a kiindulási pontba.

• Periódus idő:

  Egy periódus megtételéhez szükséges idő.

      

  Jele: T
  [T] = s

• Fordulatszám:

  Egy másodperc alatt megtett periódusok száma.

        

Jele: n

Azt a körmozgást nevezzük egyenletesnek, ahol teljesül, hogy a test egyenlő idők alatt egyenlő íveket fut be, tehát kétszer, háromszor, hosszabb idő alatt a befutott ív is kétszer, háromszor hosszabb.

Kerületi sebesség

• Iránya minden pillanatban érintőirányú.
• Nagyságát megkapjuk, ha az ívet osztjuk az ív megtételéhez szükséges idővel.



illetve a teljes körív osztva a körív megtételéhez szükséges idővel.



• A kerületi sebesség nagysága függ a sugártól.

Szögsebesség

Megkapjuk, ha a radiánban kifejezett szögelfordulást osztjuk a szögelforduláshoz szükséges idővel.

Jele: ω

• Az egyenletes körmozgást végző test kétszer, háromszor hosszabb idő alatt, kétszer, háromszor nagyobb szöggel fordul el.
• Így a szögelfordulás és a szögelforduláshoz szükséges idő között egyenes arányosság van. (α ~ t). A kettő hányadosa egyenletes mozgás esetén állandót határoz meg. Ezt az állandót nevezzük szögsebességnek.

A kerületi sebesség és a szögsebesség kapcsolata egyenletes mozgás esetén

A kerületi sebesség egyenesen arányos a sugárral, az arányossági tényező a szögsebesség.

Centripetális gyorsulás

• Az egyenletes körmozgást végző test sebességének nagysága nem változik, de iránya minden pillanatban más.

• Ebből az is következik, hogy a sebességvektor változik. Ennek következménye, hogy az egyenletes körmozgás gyorsuló mozgás.
• A sebességvektor időegységre történő megváltozását centripetális gyorsulásnak nevezzük.

  Jele: a_cp

  

  Centripetális gyorsulás nagyságának levezetése

  A sebességvektorok által meghatározott háromszög és a sugár valamint a húr által meghatározott háromszögek egymáshoz hasonlóak. Ezért oldalaik aránya megegyezik.

  

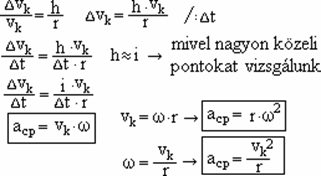
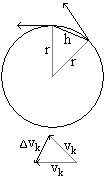
  A centripetális gyorsulás állandó nagyságú és iránya minden pillanatban a kör középpontja felé mutat. (V_k-ra merőleges!)

Dinamikai leíráskor azt vizsgáljuk, hogy milyen eredő erőnek kell egy pontszerű testre hatni, hogy az egyenletes körmozgást végezzen.
A dinamikai feltétel Newton II. törvényéből vezethető le.
F_e = m ∙ a → F_cp = m ∙ a_cp
Egyenletes körmozgásnál az eredő erőt centripetális erőnek nevezzük, a gyorsulást pedig centripetális gyorsulásnak.

Egy pontszerű test akkor végez egyenletes körmozgást, ha rá olyan eredőerő hat, amelynek nagysága állandó, és iránya minden pillanatban a kör középpontja felé mutat.

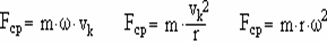
Példák egyenletes körmozgásra:

• Lemezjátszó korongjának egy pontja, ha az állandó szögsebességgel forog.
• Állandó sebességgel haladó autó kerekének egy pontja (nem a tengely).
• Óriáskerék egyik kocsija.

• A mozgás pályája a kör.
• Egyenletesen változó körmozgásnál, a kerületi sebességnek nemcsak az

iránya, de a nagysága is változik.

Pl.: Gyorsuló körmozgás

A kerületi sebességvektor időegységre eső megváltozását érintő irányú gyorsulásnak nevezzük. Jele: aé

• Az érintő irányú gyorsulás számmértéke kifejezi, hogy 1 másodperc alatt mennyivel változik meg a kerületi sebességnek a nagysága.

• Az érintő irányú gyorsulás mindig a körpálya érintőjének irányába mutat.

 

Szöggyorsulás: Egyenletesen változó körmozgásnál a szögsebesség az idővel arányosan változik.

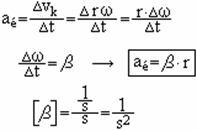
A szögsebességnek időegységre eső megváltozását szöggyorsulásnak nevezzük.
Jele:

Az érintő irányú gyorsulás egyenesen arányos a sugárral, az arányossági tényező a szöggyorsulás.

Kísérleti összeállítás egyenletesen változó körmozgás létrehozására

Függőleges tengelyre erősített korongot úgy hozunk forgó mozgásba, hogy a korong kerületére csavart fonalat csigán átvezetjük, és a végére m tömegű testet erősítünk.

• A kísérleti összeállításban az m tömegű test egyenletesen változó mozgást végez függőleges egyenes mentén.
• Ennek köszönhetően a korong pontjai is egyenletesen változó mozgást végeznek, de körpálya mentén.

Mi csak a korong egy kerületi pontját vizsgáljuk, ami így egyenletesen gyorsuló körmozgást végez.

• Az m tömegű test egyenes vonalú egyenletesen változó mozgását leíró kinematikai egyenletekből levezethető a korong bármely kerületi pontjának mozgásegyenlete. Így jutunk el az egyenletesen változó körmozgást végző test kinematikai egyenleteihez.

Amíg az m tömegű test h utat tesz meg, addig a korong pontjai ugyanakkora ívvel fordulnak el. Egyenletesen változó körmozgásnál a szögelfordulást e két bekeretezett képlet segítségével fejezhetjük ki.

Pontszerű test egyenletesen változó körmozgásához olyan eredő erő szükséges, amely két komponensből áll.

Érintő irányú erő

• a pálya menti sebességet változtatja,
• nagysága állandó,
• iránya mindig érintő irányú.

Centripetális erő

• körpályán való maradáshoz szükséges erő,
• nagysága az idő négyzetével arányosan változik,
• iránya mindig sugár irányú.

Az eredő erőt Pitagorasz-tétellel számoljuk ki.

Fé = m ∙ aé = m ∙ r ∙ β = áll.	(aé = r ∙ β)
Fcp = m ∙ acp = m ∙ ωt2 ∙ r = m ∙ r ∙ β2 ∙ t2 = változó	( mert t2 változik!)

Példák egyenletesen változó körmozgásra

• Egyenletesen gyorsuló autó kerekének egy pontja.
• A fúrófej egy pontja a fúró bekapcsolásakor és leállításakor.
• Kerekeskút kerekének egy pontja, ha a vízzel megtelt vödör gyorsulva mozog lefelé.

Ha egy tengellyel ellátott merev testre olyan erő hat, aminek a hatásvonala nem megy át a forgástengelyen, akkor a merev test forgómozgást végez.

Az erő által létrehozott forgatónyomaték egyenesen arányos a szöggyorsulással.

A kettő hányadosa egy állandót határoz meg, amelyet a merev test tengelyre vonatkoztatott tehetetlenségi nyomatékának nevezünk.

Jele:

A forgómozgást leír

A tehetetlenségi nyomaték értéke nemcsak a test tömegétől, hanem a tengelyhez viszonyított tömegeloszlástól is függ. Bármely forgó testnek a forgástengelyhez viszonyított tehetetlenségi nyomatékát megkapjuk, ha az egyes tömegpontoknak forgástengelytől mért távolság négyzetét szorozzuk a tömegpont tömegével, majd ezeket összegezzük.

A forgómozgást leíró dinamikai törvény

A forgatónyomaték egyenesen arányos a szöggyorsulással, az arányossági tényező a tehetetlenségi nyomaték.

Ha egy tengellyel ellátott test forgómozgást végez, akkor a mozgásából származó energiát forgási energiának nevezzük.

A forgási energia egyenesen arányos a szögsebesség négyzetével, az arányossági tényező a tehetetlenségi nyomaték fele.

Egy tengely körül forgó test forgásmennyiséggel rendelkezik, és ezt a forgásmennyiséget perdületnek nevezzük. Jele: N

A perdület a tehetetlenségi nyomaték és a szöggyorsulás szorzatával értelmezett fizikai mennyiség. Forgó test perdületét forgató nyomaték változtatja meg. A változás mértéke attól függ, hogy mekkora forgatónyomaték, és mennyi ideig hat rá.

Mindez a forgómozgás alapegyenletéből levezethető:

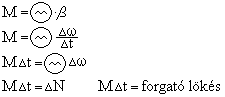
	Perdülettétel A forgató lökés megegyezik a perdület megváltozásával.
	Perdület megmaradásának törvénye Zárt mechanikai rendszerben, amikor egy forgó testre nem hat forgatónyomaték, akkor a perdület állandó.