1. A rezgőmozgás fogalma

    A rugóra függesztett testet, ha egyensúlyi helyzetéből kimozdítjuk, akkor két szélső helyzet között periodikus mozgást végez. Hasonló mozgást végez az l hosszúságú fonálra függesztett test, vagy a víz tetején lévő habszivacs, ha egyensúlyi helyzetéből kimozdítjuk.

    Rezgőmozgásról akkor beszélünk, ha egy testet az egyensúlyi helyzetéből kimozdítunk, és ennek köszönhetően a test két szélső helyzet között periodikus mozgást végez.

    A rezgőmozgás maximális kitérését vizsgálva két fajta rezgőmozgást különböztetünk meg:

    1. Csillapítatlan rezgőmozgás:
      Időben állandó a maximális kitérés (idealizált eset).
    2. Csillapított rezgőmozgás:
      A maximális kitérés időben csökken.
  2. Rezgőmozgás leírását segítő mennyiségek
    Periódus: A mozgás egy periódusának nevezzük a pályának azt a szakaszát, amikor a test a pálya egy pontjából elindul, a két szélső helyzetet érinti, és visszatér a kiindulási pontba.
    Periódus idő: Egy periódus megtételéhez szükséges idő.
    Jele: T  [T] = s
    Frekvencia: Egy s alatt megtett periódusok száma.
    Jele: f  [f] = 1/s (Hz)
    Amplitúdó: Az egyensúlyi helyzethez viszonyított maximális kitérés.
    Jele: A  [A] = m
  3. Kapcsolat az egyenletes körmozgás és a harmonikus rezgőmozgás között

    Ha egy rugóra függesztett test rezgését vizsgáljuk, és azonos időközönként megfigyeljük a kitérést, akkor azt tapasztaljuk, hogy a kitérés az idő szinuszos függvénye lesz.

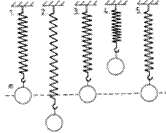
    Az olyan rezgőmozgást, ahol teljesül, hogy a kitérés az idő szinuszos függvénye harmonikus rezgőmozgásnak nevezzük.

    Ha az egyenletes körmozgást végző test mozgását a síkjából vizsgáljuk, akkor egy olyan rezgőmozgást látunk, ahol a kitérés az időnek szinuszos függvénye.

    Referencia körnek nevezzük annak az egyenletes körmozgást végző testnek a pályáját, amelynek sugara megegyezik a vizsgált rezgőmozgás amplitúdójával, fordulatszáma a rezgőmozgás frekvenciájával.

  4. A harmonikus rezgőmozgás kinematikai egyenletei

    A harmonikus rezgőmozgás kinematikai egyenletei abból a gondolatból vezethetők le, hogy az egyenletes körmozgást végző test mozgását a síkjából nézve harmonikus rezgőmozgásnak látjuk.

    Harmonikus rezgőmozgás kitérés-idő függvénye

    Az egyenletes körmozgást végző test pillanatnyi helyzetének függőleges irányú komponense a harmonikus rezgőmozgás kitérésével egyezik meg.

    y = r ∙ sinα
    Rezgőmozgás esetén: r = A

    y = A ∙ sinα  α = ω ∙ t

    y = A ∙ sin ω ∙ t
    y = A ∙ sin 2π∙f ∙ t
    y = A ∙ sin 2π/T ∙ t

    Harmonikus rezgőmozgás sebesség-idő függvénye

    Az egyenletes körmozgást végző test kerületi sebességének függőleges irányú komponense megegyezik a harmonikus rezgőmozgást végző test pillanatnyi sebességével.

    v = vk ∙ cosα

    v = r ∙ ω ∙ cosα

    v = A ω ∙ cos ω ∙ t
    v = A ω ∙ cos 2π∙f ∙ t
    v = A ω ∙ cos 2π/T ∙ t
    Ha α = 0° akkor maximális a sebesség: vmax = A ω
    Ha α = 180° akkor a sebesség: |vmax| = A ω
    Ha α = 90° + k∙360° v = 0
    Ha α = 270° + k∙360° v = 0

    Az egyensúlyi helyzetben a rezgőmozgást végző test sebessége maximális, a maximális kitérésnél nulla.

    Harmonikus rezgőmozgás gyorsulás-idő függvénye

    Az egyenletes körmozgást végző test centripetális gyorsulásának függőleges irányú komponense megegyezik a harmonikus rezgőmozgást végző test gyorsulásával.

    |a| = acp ∙ sinα
    |a| = r ω2 ∙ sinα
    |a| = A ω2 ∙ sinα    

    Mivel:
    y = A ∙ sinα → a = - y ω2

    A gyorsulás egyenesen arányos a kitéréssel, de vele ellentétes irányú. Erre utal a mínusz előjel.

    a= - A ω2 ∙ sinα
    a= - A ω2 ∙ sin ω ∙ t
    a= - A ω2 ∙ sin 2π∙f ∙ t
    a= - A ω2 ∙ sin 2π/T ∙ t

    A rezgőmozgást végző test gyorsulása akkor maximális, ha

    |sinα| = 1 → |amax|= A ω2

    A rezgőmozgást végző test gyorsulása szélső helyzetekben maximális, és egyensúlyi helyzetben nulla.

  5. A harmonikus rezgőmozgás dinamikai feltétele

    Amikor egy mozgás létrejöttének dinamikai feltételét vizsgáljuk, akkor azt nézzük meg, hogy az adott mozgást milyen erő hozza létre.

    A harmonikus rezgőmozgás dinamikai feltételét is Newton II. törvényéből vezethetjük le.


    Harmonikus rezőmozgást olyan eredőerő hoz létre, amely a kitéréssel arányos, de vele ellentétes irányú.

    Rugóállandó (direkciós erő)

    A rugóállandó számértéke megmutatja, hogy a rugó vagy rugalmas test egységnyi megnyúlását mekkora eredőerő hozza létre.

  6. A harmonikus rezgőmozgás periódusidejének levezetése

    A levezetéskor a rugóállandó összefüggéséből indulunk ki.

    A rezgőmozgás periódusideje függ a mozgást végző test tömegétől és a rugóállandótól, de nem függ a mozgás amplitúdójától.

  7. A rezgőmozgás energetikai leírása

    Egy m tömegű testet rugó segítségével falhoz erősítünk. A test és a talaj között nincs súrlódás. A testet egyensúlyi helyzetéből y távolságra kitérítjük. Ehhez erőre van szükség, és az erő által végzett munka a test energiáját növeli.
    → Az általunk kifejtett erő a kitéréssel arányos.

    Ha az erőt ábrázoljuk az elmozdulás függvényében, akkor a grafikon alatti terület mérőszáma az általunk végzett munka mérőszámát adja, ami a rugalmas energiával is megegyezik.

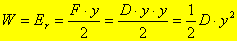
    A rugalmas energia egyenesen arányos a hosszváltozás négyzetével, az arányossági tényező a rugóállandó fele.

    Mechanikai energia megmaradásának törvénye rezgőmozgás esetén

    Rugóhoz erősített testet az egyensúlyi helyzetéből amplitúdónyi távolságra kitérítjük, majd magára hagyjuk. Bizonyítható, hogy a pálya különböző pontjaiban a rezgőmozgást végző test összes energiája állandó.

    Bizonyítani lehet hogy az összes energia a pálya bármely pontján állandó.


  8. A matematikai inga

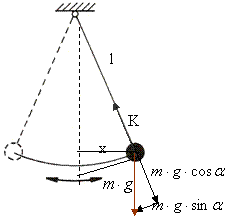
    A matematikai inga vagy más néven fonálinga egy l hosszúságú fonálból és egy pontszerű m tömegű testből áll. Ha a fonalat felfüggesztjük, és a pontszerű testet kitérítjük, akkor a test két szélső helyzet között periodikus mozgást végez. Ez a mozgás kis kitérés esetén (közelítőleg 5°) harmonikus rezgőmozgásként írható le.

    A fonálinga mozgása összetett mozgás, mert a test két szélső helyzet között, körív mentén végzi a mozgást (rezgőmozgás és körmozgás).

    Körmozgáshoz szükséges erő: Fcp = K-mg cos α (a körmozgás nem egyenletes, mert a szög változik)

    A harmonikus mozgást: F = mg cos α erőkomponens hozza létre.

     
      ahol x a kitérés (i~x kis szögek esetén)

    Az érintő irányú erő komponensről belátható, hogy a kitéréssel arányos, de vele ellentétes irányú, ezért ez az erőkomponens felelős a fonálinga harmonikus mozgásáért.

    A fonálinga lengésidejének (periódusidejének) meghatározása

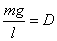
    Ami a fonálingánál 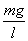 hányados, az a rugónál a rugóállandó.




    A periódusidő a fonál hosszától, és az adott helyen a nehézségi gyorsulástól függ, nem függ a test tömegtől és az amlitúdótól.

  9. Csillapított rezgések

    Csillapított rezgésekről akkor beszélünk, ha a rugóerőn kívül más fékezőerő is hat a testre. Ilyenkor az amplitúdó időben csökken, de a periódus ideje nem változik. A rezgőmozgást befolyásoló két fontos fékezőerő:

    Súrlódási erő: ilyenkor a csökkenő amplitúdók a kitérés idő grafikonon egyenesre illeszkednek.
    Közgellenállási erő: ilyenkor az amplitúdók csökkenése exponenciális.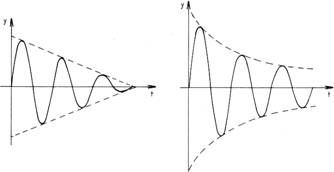

  10. Kényszerrezgés, rezonancia

    Kényszerrezgést akkor végez a test, ha egy periódikusan változó külső erő is hat rá.

    Ha a kiskocsit kitérítjük az egyensúlyi helyzetéből, akkor egy saját frekvenciával rezgőmozgást fog végezni. Ezt a frekvenciát csak a kocsi tömege és a rugóállandók határozzák meg. Ha a kereket állandó fordulatszámmal kezdjük el mozgatni, akkor a kiskocsi rövid időn belül ugyanezzel e frekvenciával mozog. Ilyenkor a kereket gerjesztő rendszernek, a rugók között lévő kiskocsit pedig, gerjesztett testnek nevezzük.

    A kényszerrezgés speciális formája a rezonancia. Rezonancia akkor következik be, ha a gerjesztő frekvenciája megegyezik a rezgőképes rendszer saját frekvenciájával. Ilyenkor a rezgő rendszer megfelelő ütemben kap energia-adagokat, amely az amplitúdó növekedésében figyelhető meg.