- A hullám fogalma, csoportosítása és jellemzői
- A mechanikai hullám fogalma
Hullámmozgás akkor alakul, ki ha egy külső erő által létrehozott, deformációs állapot, egy közegben tovább terjed.
Hullámmozgás csak rugalmas és rezgőképes közegben alakul ki. A zavar terjedési sebességét a rugalmas kapcsolat erőssége határozza meg. Rezgőmozgás során impulzus illetve energia terjed a közegben és nem az anyagi részek, végeznek haladó mozgást.

A rugó végét minkét esetben periodikusan mozgatjuk. A belső erők következtében a rugó távolabbi pontjai is átveszik ezt a periodikus mozgást. Így alakul ki a képen látható hullám.
- Hullámfajták
A továbbiakban mi csak harmonikus hullámokkal foglalkozunk. Ilyen hullámok akkor jönnek létre, ha a rugalmas és rezgőképes közegben a deformációs állapotot harmonikus rezgőmozgás hozza létre.
- Kiterjedés szerinti csoportosítás
- Egydimenziós hullámok vagy vonal menti hullámok. Pl.: gumikötélen terjedő hullám.
- Kétdimenziós hullám vagy felületi hullám. Pl.: vízfelületén kialakuló hullám.
- Háromdimenziós vagy térbeli hullám. Pl.: hanghullám.
- Rezgésirány szerinti csoportosítás
- Tranzverzális hullám
- A részecskék rezgésének iránya merőleges a zavar terjedésének irányára.
- Egy tranzverzális hullámban hullámhegyek és hullámvölgyek váltogatják egymást.
- Egy hullámhegy és egy hullámvölgy együttese a hullámhossz (λ). Amíg a zavar hullámhossznyi utat tesz meg egy periódusidő (T) telik el.
- Csak szilárd közegben alakul ki.
- A zavar terjedési sebessége:
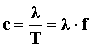
- Longitudinális hullám
- A részecskék rezgőmozgásának iránya megegyezik a zavar terjedésének irányával.
- A longitudinális hullámban egymás mellett lévő sűrűsödés és ritkulás alkotja a hullámhosszt.
- Mindhárom halmazállapotban kialakul.
- Kiterjedés szerinti csoportosítás
- A hullámmozgás jellemzői
- Amplitúdó
Jele: A
Mértékegysége:
A hullámmozgásban résztvevő részecskék rezgőmozgásának legnagyobb kitérése. - Hullámhossz
Jele: λ
Mértékegysége:
A közegben egymás mellett lévő azonos fázisú pontok távolsága egy adott pillanatban. - Periódusidő
Jele: T
Mértékegysége:
Az az időtartam, amely alatt a közegben lévő zavar hullámhossznyi utat tesz meg. A periódusidő alatt a közeg minden pontja egy teljes rezgést végez. - Rezgésszám
Jele: f
Mértékegysége:
A hullámmozgásban részt vevő pontok rezgésének a frekvenciája. Ez megegyezik a hullámforrás frekvenciájával. - A hullám terjedési sebessége
A hullámterjedési sebességét fázissebességnek is nevezzük.
Jele: c
Mértkegysége:
A terjedési sebesség számértéke megmutatja, hogy egy másodperc alatt a közegben terjedő zavar milyen távolságot tesz meg.

- Amplitúdó
- A hullámok polarizációja
Polarizációról akkor beszélünk, ha egy alkalmasan megválasztott eszköz segítségével különböző rezgésirányú hullámok közül egyfajta rezgésirányú hullámot kiszűrünk.

- Egy gumikötelet átfűzünk egy függőleges résen.
- A kötél végét kör mentén periodikusan mozgatjuk.
- Így olyan hullám keletkezik, amelyben a terjedés irányára merőlegesen sokféle rezgésirány megtalálható.
- A résen már csak az a hullám halad át, melynek rezgési iránya a résiránnyal egyezik meg.
Így sikerül a sokféle rezgésirányú hullámok közül egyfajta rezgésirányú hullámot kiszűrni. Az így kiválasztott hullámot síkban poláros hullámnak nevezzük.
Csak a tranzverzális hullám polarizálható.
- A mechanikai hullám fogalma
- Egydimenziós hullámok
- visszaverődése
Rögzített végről:
Rögzített végről a hullám ellentétes fázisban verődik vissza. Ennek azaz oka, hogy a hullámban terjedő energiának a visszaverődés után is meg kell maradnia. Amikor a deformációs állapot a rögzített véghez érkezik, akkor a gumikötél erőt fejt ki a falra, a fal ugyanilyen nagyságú, de ellentétes irányú erőt fejt ki a gumikötélre. Ez az erő lesz az, ami a gumikötelet ellentétes fázisba lendíti át.

Szabad végről:
Szabad végről a hullám azonos fázisban verődik vissza, mert amikor a zavar elérkezik a szabad véghez, akkor a rugalmatlan kapcsolat miatt nincs olyan erő, amely ellentétes fázisba lendítené a gumikötelet.

- hullámok interferenciája
A hullámok találkozásánál tapasztalható fizikai jelenséget interferenciának nevezzük.
Az interferencia eredménye lehet a tartósan fennmaradó hullámjelenség, amit interferenciaképnek szokás nevezni.
Az interferenciaképet létrehozó hullámokat koherens hullámoknak nevezzük.
Két hullám akkor koherens, ha időben állandó fáziskülönbséggel találkoznak.- Azonos fázisban induló azonos frekvenciájú vonal menti hullámok interferenciája

Vonal menti hullámok interferenciája során eredő hullám jön létre. Ilyenkor a pontok kitérése mindenütt és minden pillanatban a találkozó hullámok adott pontbéli kitérésének előjeles összege.
Azonos fázisban induló azonos frekvenciájú hullámok interferenciájuk során akkor erősítik egymást, ha azonos fázisban találkoznak. Ennek az a feltétele, hogy a hullámok által megtett utak különbsége a fél hullámhossz páros számú többszöröse legyen:

Azonos fázisban induló azonos frekvenciájú hullámok akkor gyengítik, vagy oltják ki egymást, ha ellentétes fázisban találkoznak. Ennek az a feltétele, hogy a hullámok által megtett utak különbsége a fél hullámhossz páratlan számú többszöröse legyen:

- Ellentétes fázisban induló azonos frekvenciájú hullámok interferenciája
 Ellentétes fázisban induló azonos frekvenciájú hullámok interferenciájuk során akkor erősítik egymást, amikor hullámok által megtett utak különbsége a fél hullámhossz páratlan számú többszöröse.
Ellentétes fázisban induló azonos frekvenciájú hullámok interferenciájuk során akkor erősítik egymást, amikor hullámok által megtett utak különbsége a fél hullámhossz páratlan számú többszöröse.
Ugyanilyen feltételek mellett induló hullámok akkor gyengítik vagy oltják ki egymást, ha a megtett utak különbsége a fél hullámhossz páros számú többszöröse.

- Haladó és visszaverődő hullámok interferenciája
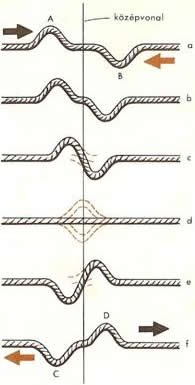
A rögzített végű gumikötélen hullámhegyet indítunk el. Amikor ez a zavar rögzített végről ellentétes fázisban visszaverődik, akkor egy újabb hullámhegyet indítunk vele szemben. Ez a két deformációs állapot közeledik egymáshoz, és úgy tűnik mintha akadály nélkül, áthaladnak egymáson.
Ennek ellentmond az a tény, hogy a gumikötélnek lesz egy olyan pontja, amely nem vesz részt a hullámmozgásban, mert minden pillanatban nyugalomban lesz. Erre a pontra a hullámok közeledésekor két azonos nagyságú, de ellentétes irányú erő hat. Ez a pont rögzített végként viselkedik, és erről az oda érkező hullámok ellentétes fázisban verődnek vissza.
- Azonos fázisban induló azonos frekvenciájú vonal menti hullámok interferenciája
- állóhullámok kialakulása
Állóhullám akkor alakul ki, ha egy haladó és egy visszaverődő periodikus zavar találkozik.

Ilyenkor lesznek a közegnek olyan pontjai, amelyekre minden pillanatban két ellentétes irányú, de azonos nagyságú erő hat. Ezek csomópontoknak nevezzük, amelyek mindig nyugalomban lesznek.
Két szomszédos csomópont távolsága a hullámhossz fele. A csomópont két oldalán a részecskék rezgésének iránya ellentétes.
A maximális kitérésű helyeket duzzadási helyeknek nevezzük ezek távolsága is fél hullámhossz.
- visszaverődése
- Hullámok matematikai leírása
A hullámok matematikai leírásánál olyan egyenleteket kell felírni, amelyekből bármely pillanatban ki tudjuk számolni a hullámban résztvevő részecskék kitérését, sebességét, gyorsulását.
Próbáljuk meghatározni a hullámforrástól x távolságra lévő részecske a hullámkeltés kezdetétől számított t idő múlva mekkora kitéréssel rendelkezik!

Vizsgáljuk a hullámforrástól x távolságra lévő pont mozgását. Ha a zavar terjedési sebessége c akkor a hullámforrás által elindított zavar
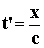 idő múlva érkezik el a vizsgált P ponthoz.
idő múlva érkezik el a vizsgált P ponthoz.
Tehát adott pillanatban a hullámforrástól x távolságra lévő pont ugyanazt a mozgást végzi, mint amelyet a hullámforrás végzett t’ idővel korábban. A hullámforrástól x távolságra lévő pont kitérését a következő egyenletekkel számoljuk ki:

- Térbeli hullámok
- Huygens-Fresnel-elv
A térbeli hullámok kialakulásának magyarázatát Huygens fogalmazta meg 1678-ban.

 A hullámok úgy terjednek, hogy a hullámfelület minden pontjából elemi hullámok indulnak, ezen elemi hullámok burkoló felülete lesz az új hullámfelület.
A hullámok úgy terjednek, hogy a hullámfelület minden pontjából elemi hullámok indulnak, ezen elemi hullámok burkoló felülete lesz az új hullámfelület.Fresnel 1819-ben a Haygens-elvben szereplő burkolófelületnek az interferencia jelenséggel adott értelmet.
A Haygens-Fresnel-elv szerint a hullámtér minden pontja az elemi hullámok kiindulópontja. A hullámtérben megfigyelhető jelenségek az elemi hullámok interferenciája miatt jönnek létre. - felületi és térbeli hullámok viselkedése új határfelületen
A térbeli hullámok új határfelülethez érkezve
- részben elnyelődnek
- részben visszaverődnek
- részben megtörnek
- A hullámok elnyelődése
A hullámok elnyelődése során az új közeghatárhoz érkező hullám energiájának egy részét átadja az új közegnek. Így az új közeg részecskéi is rezgőmozgásba kezdenek.
- A hullámok visszaverődése
Ha a hullám egy olyan közeg határfelületéhez érkezik, amely nem rugalmas és rezgőképes, akkor erről a határfelületről visszaverődik.
Néhány elnevezés
- Beesési pont
A sugár és a visszaverő felület találkozási pontja.
- Beesési merőleges
A beesési pontba képzelt, a közeghatárra merőleges egyenes.
- Beesési szög
A beeső sugár és a beesési merőleges által bezárt szög.
- Visszaverődési szög
A visszavert sugár és a beesési merőleges által bezárt szög.
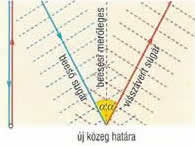
Célszerű egy keskeny, egyenes hullám visszaverődését vizsgálni az új közeg határáról. Pl. vízfelületen egy vonalzó periodikus mozgatásával indítunk el egy felületi hullámot. A közegben a zavar terjedési sebessége c.
- A haladó és a visszaverődő hullám frekvenciája is f, így visszaverődés során a hullám hullámhossza (λ) sem változik.
- Ha a hullámfelület minden pontja egyszerre éri el a visszaverő felületet, akkor a hullám ugyanazon az úton verődik vissza, mint amelyen érkezett. Tehát, a merőlegesen beeső hullám merőlegesen verődik vissza.
- Ha a hullámfelület pontjai nem egyszerre érik el a visszaverő felületet, akkor a beesési szög megegyezik a visszaverődési szöggel.
Bizonyítás

- Amikor a hullámfelület első pontja elérkezik a visszaverő felülethez akkor a legtávolabbi pont még
 távolságra van.
távolságra van.
(t jelölje azt az időt, ami a hullámfelület első és utolsó pontjának a felülethez való érkezése között eltelt, c az adott közegben a zavar terjedési sebessége).
- Ilyenkor elemi hullámok indulnak visszafelé.
- Mire a legtávolabbi pont is eléri a visszaverő felületet, addigra a legelső elemi hullámok már
 távolságra jutottak.
távolságra jutottak. - A szerkesztésből látszik, hogy a két derékszögű háromszög egybevágó (AECΔ = AEFΔ, ezért a és b egyenlő nagyságúak.
Ebből következik, hogy a hullámok visszaverődésekor, a beesési és visszaverődési szög megegyezik.
- Beesési pont
- A hullámok törése

A hullámok törése akkor következik be, ha az egyik közegben terjedő hullám átlép egy másik olyan rugalmas és rezgőképes közegbe, amelyben más lesz a terjedési sebesség. Ilyenkor a hullám terjedési iránya megváltozik, ha nem merőlegesen érkezett a határfelületre.
Az első közegben c1 a másodikban c2 a hullám terjedési sebessége.
A hullám törésére a Snellius-Descartes-törvény igaz, mely szerint:
A hullám törésénél a beesési és a törési szög szinuszának a hányadosa megegyezik az egyes közegekben mérhető terjedési sebességek hányadosával, ami a második közegnek az első közegre vonatkoztatott törésmutatóját adja.Bizonyítás

Amikor az első közegben a hullámfelület első pontja eléri a közeghatárt, akkor elemi hullámok, indulnak a második közeg felé. Ilyenkor a legtávolabbi pontnak
 utat kell megtenni.
utat kell megtenni. (t jelölje azt az időt, ami a hullámfelület első és utolsó pontjának a felülethez való érkezése között eltelt, c1 és c2 az adott közegben a zavar terjedési sebessége).
Mire ez a deformációs állapot is elérkezik a közeghatárhoz, addigra a legelső pontból kiinduló elemi hullámok már
 távolságra jutottak az új közegben. Hullám törésekor frekvenciája nem változik.
távolságra jutottak az új közegben. Hullám törésekor frekvenciája nem változik.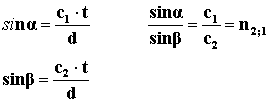
- Felületi és térbeli hullámok interferenciája
Felületi és térbeli hullámok is létrehozhatnak interferenciaképet, ha a találkozó hullámok koherensek.



Az interferenciakép létrejöttének azonban itt is szigorú feltételei vannak. Pl. a vízfelületen két egymástól távol lévő, de együtt mozgó tűvel keltett körhullámok interferenciája hiperbolák mentén hoz létre hullámhegyeket és hullámvölgyeket.
Két hullám a hullámtér azon pontján hoz létre maximális erősítést, ahol a hullámok azonos fázisban találkoznak (hullámhegy hullámheggyel, hullámvölgy hullámvölggyel, sűrűsödés sűrűsödéssel, ritkulás ritkulással)
Ilyen feltételek mellett induló hullámok akkor találkoznak azonos fázisban, ha a hullámok által megtett utak különbsége a félhullámhossz páros számú többszöröse.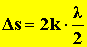
Két azonos frekvenciájú, azonos fázisban induló hullám maximális gyengítése akkor következik be, ha a hullámok által megtett utak különbsége a félhullámhossz páratlan számú többszöröse.
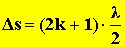
- Az elhajlás jelensége

Hullámok elhajlásáról akkor beszélünk, hogyha a hullám útjába egy olyan akadályt helyezünk, amelyben lévő nyílás közel hasonló mérető, mint a hullámhossz. Ilyenkor az akadály mögötti térrészben is észlelünk hullámjelenséget.
Ennek, azaz oka, hogy az akadály nyílásánál lévő részecskék, a belső erők következtében átveszik a rezgőmozgást, és elemi hullámokat indítanak el. Ezek burkoló felülete lesz az akadály mögötti részben észlelhető új hullámfelület.A hullám elhajlása során a hullám intenzitása jelentősen csökken.


- Huygens-Fresnel-elv
- A hanghullámok jellemzői
- A hanghullámok keletkezése
A hang rugalmas és rezgőképes közegben terjedő olyan hullám, ami hallószervünkben hangérzetet kelt. Az emberi fül 20-20000 Hz terjedő mechanikai rezgéseket képes érzékelni.
Ha a frekvencia kisebb, mint 20 Hz, akkor hangot infrahangnak nevezzük. Néhány halfajta ez alapján tájékozódik. Ha frekvencia nagyobb, mint 20000 Hz akkor ultrahangokról beszélünk. Ez alapján tájékozódnak a denevérek, és a kutyák is halják.
- Tiszta zenei hang
- a hangforrás rezgése szinuszos
- a keltett hullámok rezgése periodikus és szinuszos
- csak egyfajta frekvenciájú hangból áll
- pl.: a hangvilla által keltett hang (440Hz)

- Zenei hang
- az alaphangok mellett a felhangok is megszólalnak különböző intenzitással
- a felhangok frekvenciája az alaphang frekvenciájának egész számú többszörösei
- zenei hangnak nem feltétlenül szükséges szinuszosnak lennie csak az a fontos, hogy periodikus legyen.


- Zörej
- szabálytalan nem szinuszos és nem periodikus rezgésű hanghullámok

- Tiszta zenei hang
- A hanghullámok jellemzői
- Hangintenzitás, hangerősség
Egységnyi idő alatt egységnyi felületre jutó hangenergia, függ a rezgéskeltő amplitúdójától.
Jele: I
- Hangmagasság
A rezgésszámtól függ, minél nagyobb a rezgésszám annál magasabb a hang.
- Hangköz
Két hang viszonylagos magasságát a rezgésszámok hányadosa méri.
A 2:1 arányú hangköz neve oktáv. - Hangszín
Attól függ, hogy az alaphangok mellett milyen más felhangok szólalnak meg, és milyen intenzitással. A hangszerek doboza, a fej csak bizonyos felhangokat erősít fel, ezért egyediek a hangszínek.
- Hangterjedési sebesség
A mechanikai hullámok terjedéshez közegre van szükség. A hang terjedési sebesség függ a hőmérséklettől és az anyag minőségétől.
- Hangintenzitás, hangerősség
- Húrok által keltett hangok
Monochordon az az eszköz, amelyen egyetlen húr található. A húron csak olyan hullámhosszúságú hullámok alakulnak ki, amelyek a fél hullámhossz egész számú többszöröse.

Alaphang
A húr által kibocsátott olyan hang, amikor a húron fél hullámhossz alakul ki.
Felhangok
Az alaphangnál kisebb hullámhosszúságú hangok.
- Sípok által keltet hangok
- Nyelvsíp

A nyelvsípban található a befúvás helyén egy olyan könnyen mozgó lemez, amely az áramló levegőben fellépő nyomáskülönbségek miatt hol nyit, hol zár. Ez a periodikus mozgás indítja el a hanghullámot.
- Ajaksíp

Ajaksípban a levegő útjának jelentős részét akadály zárja el így örvények keletkeznek. Az örvények leválása indítja el a hullámokat.
- Zártsíp

A befúvás helyével szemben a síp zárt, alaphang kibocsátása esetén a síp hossza a hullámhossz negyede.
- Nyitott síp
A be fúvás helyével szemben a síp nyitott alaphang kibocsátása esetén a síp hossza a hullámhossz fele.
- Nyelvsíp
- A Doppler-jelenség
Doppler 1842-ben elsőként írta le, hogy a hangforrás és a megfigyelő egymáshoz viszonyított mozgása, hogyan befolyásolja a hullámok észlelt frekvenciáját.
Ezt a jelenséget Doppler jelenségnek nevezzük.A leírás során használt jelölések:
c zavar terjedési sebessége a közegben vm a megfigyelő sebessége vf a forrás sebessége f0 1s alatt indult periodikus hullámok Különböző eseteket vizsgálva meghatározható a megfigyelő által észlelt frekvencia. Ettől függ, hogy milyen magasságú hangot hall a megfigyelő.
- A megfigyelő nyugalomban van (vm=0)
- és a hullámforrás közeledik a megfigyelőhöz vf sebességge
A közegben időegység alatt (pl. 1 secundum alatt) kialakult f0 hullám c-vf szakaszon helyezkedik el, így egyetlen hullám hullámhossza

A megfigyelő által észlelt frekvencia:
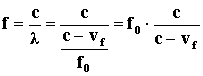
Ha a hangforrás közeledik a megfigyelő felé, az egyre magasabbnak észleli a hangot, mivel f>f0.
- és a hullámforrás távolodik a megfigyelőtől vf sebességgel
A közegben időegység alatt kialakult hullám c+vf szakaszon helyezkedik el, így egyetlen hullám hullámhossza:

A megfigyelő által észlelt frekvencia:
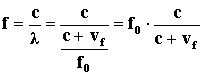
Ha a hangforrás távolodik a megfigyelőtől, az egyre mélyebbnek észleli a hangot, mivel f<f0.
- és a hullámforrás közeledik a megfigyelőhöz vf sebességge
- A hullámforrás nyugalomban van (vf=0)
- és a hullámforráshoz közeledik a megfigyelő
A hullámforrás által kibocsátott hullám hullámhossza:

A megfigyelőhöz viszonyítva a zavarterjedési sebessége:
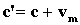
A megfigyelő által észlelt frekvencia:

Ha hangról van szó, akkor azt magasabbnak, észleljük, mivel f>f0.
- és a hullámforrástól távolodik a megfigyelő
A hullámforrás által kibocsátott hullám hullámhossza:

A megfigyelőhöz viszonyítva a zavarterjedési sebessége:

A megfigyelő által észlelt frekvencia:

Ha hangról van szó, akkor azt mélyebbnek észleljük, mivel f<f0 .
- és a hullámforráshoz közeledik a megfigyelő
- Nyugvó közegben a forrás és megfigyelő
- közelednek egymáshoz
A hullámforrás által kibocsátott hullám hullámhossza:

A megfigyelőhöz viszonyítva a zavar terjedési sebessége:
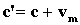
A megfigyelő által észlelt frekvencia:

Tehát az észlelő magasabb hangot hall, mivel f>f0.
- távolodnak egymástól
A hullámforrás által kibocsátott hullám hullámhossza:

A megfigyelőhöz viszonyítva a zavar terjedési sebessége:

A megfigyelő által észlelt frekvencia:

Ilyen esetben a megfigyelő mélyebb hangot hall, mivel f<f0.
- közelednek egymáshoz
- A megfigyelő nyugalomban van (vm=0)
- A hanghullámok keletkezése