- Gázhalmazállapot jellemzése
A gázhalmazállapotú anyagok viselkedésének leírása viszonylag egyszerűbb, mint a folyadékoké vagy a szilárd anyagoké, mert anyagi minőségtől függetlenül bizonyos szempontból lényegében egyformán viselkednek.
- A gázban lévő molekulák rendezetlen mozgást végeznek. Ezzel magyarázható a Tyndall által megfigyelt jelenség is.
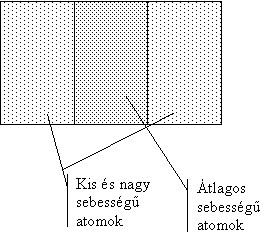
- A gáztérben lévő molekulák állandó hőmérséklet mellett is különböző sebességgel mozognak. A legtöbb molekula egy adott hőmérsékleten átlagos sebességgel mozog. Ennél nagyobb vagy kisebb sebességgel csak kevés molekula mozog. Ezt legszemléletesebben Ottó Stern bizonyította kísérletileg.
- a gázokban lévő molekulák háromfajta mozgást végeznek:
- haladó mozgást
- forgómozgást
- rezgőmozgás
- Amíg a részecskék mozgási energiája lényegesen nagyobb, mint a közöttük levő kölcsönhatásból származó energia (másodrendű kötőerők), addig a molekulák egymástól függetlenül végzik mozgásukat, a halmaz gázállapotban van.
Gázállapotban a molekulák átlagos távolsága több nagyságrenddel nagyobb, mint saját átmérőjük, így egymásra gyakorolt hatásuk kicsi, gyakorlatilag elhanyagolható.
Tyndall megfigyelte, hogy a levegőben lévő porszemek zegzugos mozgást végeznek. Ez azzal magyarázható, hogy a levegőben lévő molekulák mozognak és mozgásuk során porszemeknek, ütköznek, így a porszemek az eredő erő irányába mozdulnak el.
Ez a jelenség hasonló, mint amelyet Robert Brown, skót botanikus figyelt meg, aki 1827-ben folyadékba kevert virágport vizsgált mikroszkópjával. Megfigyelte a virágszemcsék szabálytalan mozgását, de nem tudta megmagyarázni, hogy mi okozza ezt a mozgást. A jelenség első matematikai leírását Albert Einstein adta meg.Ottó Stern kísérlete: Egy platina szálat ezüsttel vont be. A rudat belehelyezte egy nyílással rendelkező hengerbe, ezt pedig belehelyezte egy állandó szögsebességgel forgó hengerbe. A rendszert felmelegítette egy olyan állandó hőmérsékletre, amelyen az ezüst éppen párolog. A belső henger nyílását kinyitotta annyi időre, amennyi alatt a külső henger egyszer körbefordul. Egyszeri körülfordulás után a külső henger palástját levették és megvizsgálták. Azt tapasztalták, hogy az ezüstatomok nem egyenletesen csapódtak be a palást felületére.
Az első tartományban kevés ezüstatomot találtak, ebből arra következtettek, hogy nagy sebességgel kevés molekula rendelkezik.
Az utolsó tartományban is kevés atom csapódott be. Ezek érték el legkésőbb a palást felszínét, mert sebességük kicsi volt.
A legtöbb részecske átlagos sebességgel rendelkezett és a középső tartományba csapódott be.

- Ideális gázok modellje
Mérések azt mutatják, ha a gáz sűrűsége nem túl nagy, akkor a legtöbb gáz fizikai viselkedése hasonló. Ezért célszerű bevezetni egy olyan idealizált modellt, amely a gázok közös tulajdonságait tartalmazza, de az egyedi tulajdonságokat figyelmen kívül hagyja (pl. a gáz színét, szagát, stb.).
Ezt a modellt ideális gázmodellnek nevezzük, amelynek a következő tulajdonságai vannak:- a molekulák pontszerűek,
- rendezetlenül mozognak,
- tökéletesen rugalmasan ütköznek.
Leginkább a nemesgázok viselkedése hasonlít az ideális gázmodellhez.
A valódi gázokban ez a három feltétel csak közelítőleg teljesül. - Állapotjelzők
Az állapotjelzők azok a mérhető makroszkopikus jellemzői egy anyagnak, amely segítségével az anyag sajátosságai meghatározhatók.
A gázok állapotát egyértelműen meghatározó állapotjelzők a gáz:- térfogata,
- nyomása,
- hőmérséklete,
- anyagmennyisége,
- tömege.
Az állapotjelzők között vannak intenzív állapotjelzők, amelyek a folyamat során kiegyenlítődnek. Ilyenek a nyomás és a hőmérséklet.
Vannak olyan állapotjelzők, amelyek a folyamat során összeadódnak. Ezek az extenzív állapotjelzők. Ilyen a tömeg, az anyagmennység, a térfogat.
Bármely állapotjelző megváltozása — pl. hűtés — legalább egy, de inkább több állapotjelző megváltozását is maga után vonja.
Az állapotjelzők közötti összefüggés matematikai leírása az állapotegyenlet.
- Nyomás
A felületre merőleges nyomóerő és a felület nagyságának a hányadosa.
Jele: p
Mértékegysége: [p]=N/m2=Pa - Térfogat
A gázok térfogata az a térrész, amelyben a molekulák mozoghatnak.
Jele: V
Mértékegysége: [V]=m3 - Hőmérséklet
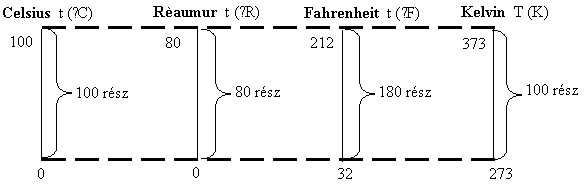
Hőmérséklet mérésére felhasználható minden olyan jelenség, amelyről tudjuk, hogy milyen függvény szerint változik a hőmérséklettel. Leggyakrabban a folyadékok térfogatváltozását szokták hőmérséklet mérésére használni.
Jele: T 
ha Kelvinben van kifejezve a hőmérséklet. t 
ha Celsius-, Rèaumur-, Fahrenheitben van kifejezve. Néhány hőmérsékleti skála
- Anyagmennyisé
A mérleggel mérhető mennyiségek nagyon sok részecskéből állnak. Az anyagmennyiség mértékegysége a mol.
Egy mol annak a rendszernek az anyagmennyisége, amely 6∙1023 db részecskét tartalmaz.
Az anyagmennyiség jele: n - Tömeg
A gáz tömegét m-mel jelöljük.
Mértékegysége: kg.
- Hőmérséklet kinetikai értelmezése
A hőmérséklet kinetikai értelmezése azt jelenti, hogy összefüggést keresünk a gázban lévő molekulák mozgása és a gáz hőmérséklete között.

Kísérlet:- Felszívunk az egyik fecskendőbe 5 cm3 tömény ammónia oldatot, a másik fecskendőbe 5 cm3 tömény sósav oldatot.
- A két fecskendő tartalmát a cső két végén egyidejűleg a csőbe juttatjuk, majd a csövet dugóval bedugjuk.
Tapasztalat:
Bizonyos idő elteltével a csőben fehér füstgyűrű keletkezik.
Magyarázat:
A gázok a csőben diffundálva találkoznak és egymással reagálva fehér NH4Cl-ot (szalmiáksót) képeznek.
A szalmiáksó kialakulásához az ammónia molekuláknak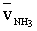 sebességgel
sebességgel 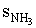 utat kellett megtenni, a hidrogén-klorid molekuláknak
utat kellett megtenni, a hidrogén-klorid molekuláknak 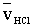 sebességgel sHCl utat kellett megtenni.
sebességgel sHCl utat kellett megtenni.


A kísérlet során megmérjük az ammónia és a hidrogén-klorid molekulák által megtett utak hosszát a találkozásig.
Az összefüggésből megállapítható, hogy a molekulák által megtett utak aránya megegyezik a molekulák átlagsebességének arányaival.
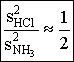
 A kísérlet során megállapítható, hogy a hidrogén-klorid és ammónia molekulák által megtett utak négyzeteinek aránya megközelítőleg
A kísérlet során megállapítható, hogy a hidrogén-klorid és ammónia molekulák által megtett utak négyzeteinek aránya megközelítőleg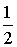 .
.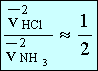
 Ebből viszont az is következik, hogy a molekulák átlagsebességének arány is
Ebből viszont az is következik, hogy a molekulák átlagsebességének arány is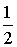 .
. 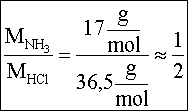

Ha a két gáz moláris tömegét összehasonlítjuk, akkor hasonló arányt kapunk, mint az átlagsebességek négyzetének aránya.
Ebből következik, hogy az ammónia és a hidrogén-klorid molekulák tömegének aránya is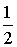 .
.

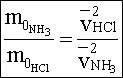
 A két jelzett arányt egyenlővé tehetjük, majd rendezzük az egyenletet.
A két jelzett arányt egyenlővé tehetjük, majd rendezzük az egyenletet.
Ezt követően mindkét oldalát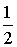 -del beszorozzuk. Így a következő összefüggést kapjuk:
-del beszorozzuk. Így a következő összefüggést kapjuk:
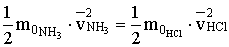
A levezetésből láthatjuk, hogy állandó hőmérsékleten különböző molekulák átlagos mozgási energiája megegyezik.
Ha csökkentjük a gázok hőmérsékletét, akkor csökken a molekulák átlagos mozgási energiája, de az soha nem lehet nulla.
Azt a képzeletbeli hőmérsékletet, amelyen a molekulák átlagos mozgási energiája nullává válna, abszolút nulla foknak nevezzük. Ez a kelvin-féle hőmérsékleti skála alappontja. Ez -273,16°C.
Ennek a hőmérsékleti skálának a bevezetése azért lényeges, mert így a molekulák átlagos mozgási energiája és a kelvinben kifejezett hőmérséklet között egyenes arányosság van.
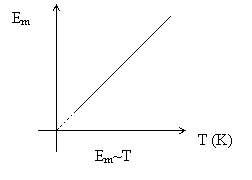
A molekulák átlagos mozgási energiája egyenesen arányos a kelvinben kifejezett hőmérséklettel, az arányossági tényező
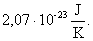
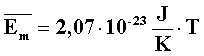
- Nyomás kinetikai értelmezése
A gázok nyomása és a gázmolekulák átlagos mozgási energiája között is összefüggés van. Ezt vizsgáljuk meg egy gondolatkísérlet során.
Gondolatban töltsünk meg egy a oldalhosszúságú, kocka alakú tartályt gázzal.
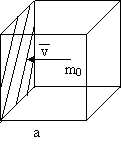
- Így a gáztartály térfogata V=a3.
- Legyen a tartályban N számú molekula.
- A molekulák tömege legyen m0.
- Tételezzük fel, hogy valamennyi molekula
átlagsebességgel rendelkezik. (
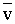 )
)
- Nagyszámú molekula esetén belátható, hogy egy adott pillanatban a tartály mindegyik lapja felé
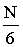 db molekula mozog.
db molekula mozog.
Elegendő a kocka alakú tartály egyetlen oldalán megvizsgálni, hogy a molekulák mozgásából adódóan mekkora lesz a nyomás érték. Mivel mindegyik oldal felé ugyanannyi molekula mozog, ugyanakkora átlagos sebességgel, mindegyik oldalon ugyanakkora lesz a nyomás.
Nézzük meg, hogy a jelzett falon mekkora nyomást hoz létre egyetlen molekula:
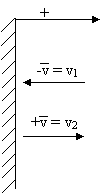
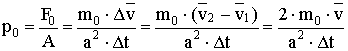
A nyomás kifejezésekor felhasználjuk a lendülettételt, amely szerint az erőlökés megegyezik a lendületváltozással. 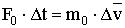
A jelzett fal felé
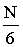 db molekula mozog. Ezek által létrehozott nyomás p.
db molekula mozog. Ezek által létrehozott nyomás p.
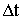 jelölje azt az időt, amely ahhoz szükséges, hogy a legtávolabbról, az az a távolságról induló molekula is elérje a jelzett falat.
jelölje azt az időt, amely ahhoz szükséges, hogy a legtávolabbról, az az a távolságról induló molekula is elérje a jelzett falat. Így
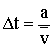 .
.Folytassuk a levezetést:
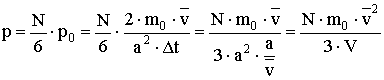
Bővítsük a törtet
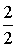 -vel!
-vel!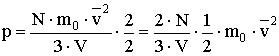
Vagyis: 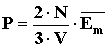 A levezetésből látszik, hogy zárt térben lévő, állandó mennyiségű ideális gáz nyomása egyenesen arányos a gázmolekulák átlagos mozgási energiájával, az arányossági tényező
A levezetésből látszik, hogy zárt térben lévő, állandó mennyiségű ideális gáz nyomása egyenesen arányos a gázmolekulák átlagos mozgási energiájával, az arányossági tényező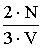 .
. - Állapotegyenlet
A gázok állapotjelzői közötti összefüggést az állapotegyenlet írja le.
Ahhoz, hogy ezt az összefüggést megkapjuk, fel kell használni a gázok nyomásának és hőmérsékletének kinematikai értelmezésekor kapott összefüggéseket. Ezek a következők:
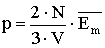
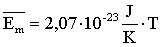
A nyomás képletébe behelyettesíthetjük a molekulák átlagos mozgási energiájára kapott összefüggést:
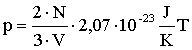
Rendezzük egy oldalra az állapotjelzőket:
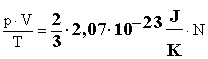
A
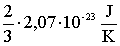 szorzat egy állandót határoz meg, melyet Boltzmann-állandónak nevezünk, és k-val jelölünk.
szorzat egy állandót határoz meg, melyet Boltzmann-állandónak nevezünk, és k-val jelölünk.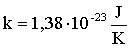
Így az állapotegyenlet egyik, gyakran használt formájához jutunk:
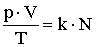
A molekulák száma kifejezhető az Avogadro-szám és mólok számának a szorzataként.
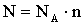
Így az állapotegyenlet egy másik formában is felírható:
A
 szorzat egy újabb állandót határoz meg, amelyet egyetemes gázállandónak nevezünk, és R-rel jelölünk.
szorzat egy újabb állandót határoz meg, amelyet egyetemes gázállandónak nevezünk, és R-rel jelölünk. 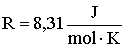
Az állapotegyenlet másik formája: 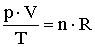
Ki lehet fejezni a mólok számát a gáz és a moláris tömeg hányadosával is:
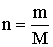 .
.Így a képlet a következőképpen módosul: 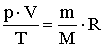
Ideális gázok állapotjelzői közötti összefüggést az állapotegyenlet írja le.
Állandó mennyiségű ideális gáz nyomásának és térfogatának szorzata osztva a kelvinben kifejezett hőmérséklettel mindig egy állandót határoz meg. Ez az állandó kifejezhető
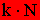 vagy
vagy 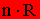 vagy
vagy  szorzattal.
szorzattal.Állandó mennyiségű ideális gáz két tetszőleges állapota közötti összefüggést fejezi ki az egyesített gáztörvény:
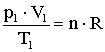
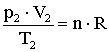

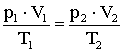
- Állapotegyenlet alkalmazása különböző állapotváltozásokra
- Izoterm állapotváltozás
Az állandó hőmérsékleten történő állapotváltozást izoterm állapotváltozásnak nevezzük.
Erre az állapotváltozásra vonatkozó törvényt egy angol és egy francia fizikus állapította meg. Az ő tiszteletükre Boyle-Mariotte-törvénynek nevezzük.
Az állapotváltozásra vonatkozó összefüggéshez mi is eljuthatunk egy gondolatkísérlet során.
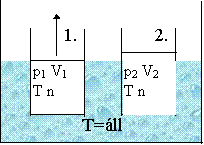
Egy hőtartályban (termosztátban) dugattyúval elzárt edényben n anyagmennyiségű gáz van.
A gáz térfogatát nagyon lassan változtatjuk, úgy, hogy közben a hőmérséklete állandó marad.
A gáz kezdeti állapotát a p1, V1, T és n, a végső állapotát a p2, V2, T és n állapotjelzők jellemzik.
Mindkét állapotra felírható az állapotegyenlet:
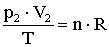
A két egyenletből következik, hogy
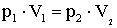
Boyle-Mariotte-törvény: Állandó mennyiségű ideális gáz izoterm állapot- változásakor a nyomás és térfogat szorzata állandó.
Állandó mennyiségű ideális gáz nyomása és térfogata között fordított arányosság van.
Izoterm állapotváltozáskor a p-V síkon ábrázolt grafikonokat izotermáknak nevezzük. Minél magasabb a hőmérséklet, annál magasabban futnak az izotermák.
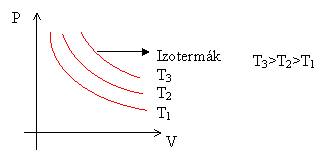
- Izobár állapotváltozás
Az állandó nyomáson történő állapotváltozást izobár állapotváltozásnak nevezzük.
Erre az állapotváltozásra vonatkozó törvényt Gay-Lussac I. törvényének is szokták nevezni. Az igazsághoz hozzátartozik, hogy Gay-Lussac valóban felfedezte ezt a törvényt, de csak harmadikként. A törvény első két felfedezője Jacques Alexandre Charles (francia fizikus) és John Dalton (angol vegyész) volt. Ez indokolja, hogy vannak olyan országok, ahol ezeket a törvényeket Charles-törvényeknek nevezik.Ismét egy gondolatkísérlettel juthatunk el az állapotváltozást jellemző összefüggéshez.

Egy súrlódás nélkül mozgó A felületű dugattyúval ellátott hengerben n anyagmennyiségű gáz van. Elkezdjük a tartályt melegíteni. A dugattyúra kívülről állandó nyomás nehezedik
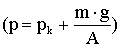 .
.Ezzel egyezik meg a hengerben lévő gáz nyomása is.
A gáz kezdeti állapotát a T1, V1, p és n, a végső állapotát a T2, V2, p és n állapotjelzők jellemzik.
Mindkét állapotra felírható az állapotegyenlet:
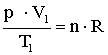
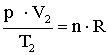
A két egyenletből következik:
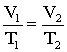
Gay-Lussac I. törvénye: Állandó mennyiségű ideális gáz izobár állapot változásakor a térfogat és a kelvinben kifejezett hőmérséklet hányadosa egy állandót határoz meg.
Ha a térfogatot a kelvinben kifejezett hőmérséklet függvényében ábrázoljuk akkor a kapott függvények az izobárok.
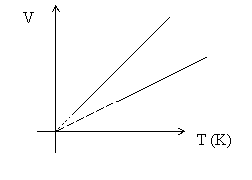
- Izoterm állapotváltozás
- Izochor állapotváltozás
Az állandó térfogaton történő állapotváltozást izochor állapotváltozásnak nevezzük.
Gondoljuk végig a következő folyamatot:

Egy V térfogatú zárt tartályban n anyag mennyiségű gázt melegítünk.
A gáz kezdeti állapotát a p1, T1, V és n, a végső állapotát a p2, T2, V és n állapotjelzők jellemzik.
Mindkét állapotra felírható az állapotegyenlet:
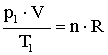

A két egyenletből következik:

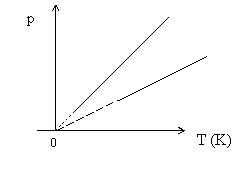
Gay-Lussac II. törvénye: Állandó mennyiségű ideális gáz izochor állapot- változásakor a nyomás és a kelvinben kifejezett hőmérséklet hányadosa egy állandót határoz meg.
Ha a nyomást a kelvinben kifejezett hőmérséklet függvényében ábrázoljuk akkor a kapott függvények az izochorok.