1. Testek elektromos állapota

    A műszálas ruha levetésekor gyakran pattogásokat hallunk, sötétben még kis szikrákat is látunk. Az egymáshoz súrlódó műszálas és pamut ruhadarabok összetapadnak, vonzzák egymást.

    Ha egy műanyag rudat szőrmével vagy papírzsebkendővel megdörzsölünk, akkor a közelében lévő apró, könnyű tárgyak elmozdulnak. Dörzsöléskor a műanyagrúd elektromos állapotba kerül.
    Hasonló jelenséget tapasztalunk, ha üvegrudat bőrrel dörzsölünk meg.

    Bármilyen anyagú test elektromos állapotba hozható, ha a sajátjától különböző anyagú testtel megdörzsöljük.

    A testek elektromos állapotát egy közvetlenül nem észlelhető anyag, az elektromos töltés okozza.

    A töltések pozitív és negatív elnevezése Benjamin Franklintól származik, aki tévesen feltételezte, hogy csak egyfajta mozgásra képes töltésfajta létezik, és ennek többletét nevezte pozitívnak, a hiányát negatívnak. Az elnevezést a mai napig megtartottuk, annak ellenére, hogy választása szerencsétlenül sikerült, hiszen a mozgásra képes elektronokról kiderült, hogy a töltésük negatív.

    Kétféle elektromos állapotot különböztetünk meg.

    Negatív elektromos állapot

    • Negatív elektromos állapotban a negatív töltéstöbblettel rendelkező test van.
    • Ilyen például a szőrmével megdörzsölt ebonitrúd, vagy a selyemmel megdörzsölt műanyagrúd.

    Pozitív elektromos állapot

    • Az elektronhiánnyal rendelkező test elektromos állapota.
    • Ilyen például a szőrmével megdörzsölt ebonitrúd.

    A semleges test mind a kétféle töltést egyenlő mértékben tartalmazza.

  2. Elektromos alapjelenségek

    Az azonos töltéssel rendelkező testek taszítják egymást.

    Ez szemléltethető úgy, hogy két műanyag rudat selyemmel vagy két üveg rudat bőrrel dörzsölünk meg, az egyiket felfüggesztjük, és a másikat közelítjük hozzá.

    Ellentétes töltéssel rendelkező testek vonzzák egymást.

    Ez a hatás mutatható be a selyemmel megdörzsölt műanyag rúd és a bőrrel megdörzsölt üvegrúd között.

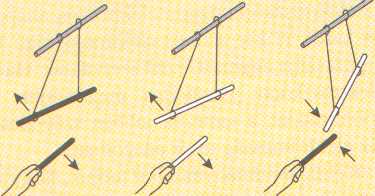
    Az elektromosan töltött test a semleges testet mindig vonzza. Amikor a test átvette a töltéseket, a töltött test eltaszítja magától. Például: a megdörzsölt műanyag rúd magához vonzza az alufólia darabkákat, majd eltaszítja magától.

    Az elektromos állapot kimutatására szolgáló eszköz az elektroszkóp.

     

    Az elektroszkóp gömbje, valamint az elektroszkópon lévő két szár, vezető anyagból készül. Ha az elektroszkóp gömbjére töltést viszünk, akkor ugyanolyan töltésűek lesznek a szárak is. Ezért az azonos töltés miatt taszítják egymást.

  3. Elektromosan töltött testek közötti kölcsönhatás
    Coulomb törvénye

    Az elektromosan töltött testek közötti kölcsönhatást Coulomb vizsgálta (1785).

     

    Eszköze a Coulomb-mérleg

    • Légüres térben, vezetőszálon egy fémgolyót helyezett el. Ezt a golyót nem lehetett elmozdítani.
    • A torziósszálra függesztett szigetelőrúd egyik végén ugyanilyen méretű fémgolyó volt.
    • Az álló golyónak bizonyos töltésmennyiséget adott, majd a torziósszál elfordításával a torziósszálon lévő golyót az álló golyóhoz érintette.
    • A két golyót r távolságra távolította egymástól. Ekkor mindkét golyón azonos töltésmennyiség volt.
    • A torziósszál a kölcsönhatás következtében elfordult.
    • Az elcsavarodás mértékéből a töltött testek közötti erőhatás meghatározható.
    • Ha a fix golyót megérintette (leföldelte), majd a mérést megismételte, most már feleakkora töltéssel, ismét meghatározhatta az erőt.
    • Sok mérést elvégezve megállapította, hogy
    Két elektromosan töltött test között fellépő erő egyenesen arányos a két töltésmennyiség szorzatával, és fordítottan arányos a köztük lévő távolság négyzetével.

    Az arányossági tényező megállapításához definiálni kellett az egységnyi töltésmennyiséget.
    Ennek meghatározása a történelem során sokat változott.

    Ma egységnyinek nevezzük azt a töltésmennyiséget, amely ugyanakkora töltésmennyiségre vákuumban egy méter távolságról 9∙109 N erővel hat.


  4. Az elektrosztatikus mezőt jellemző mennyiségek
    1. Elektromos térerősség

      Az elektromosan töltött testek maguk körül létrehozzák az anyagnak egy sajátos formáját, az elektromos mezőt. A mező rendelkezik energiával, tehetetlenséggel.

      Az elektromos mező jellemzésére szolgáló egyik fizikai mennyiség az elektromos térerősség.
      Jele E      .

      Gondolat kísérlet
      • Ha egy pontszerű Q töltés hozza létre az elektromos mezőt, akkor ezt a mezőt pontról pontra egy q próbatöltéssel (egységnyi pozitív töltés) tapogathatjuk le.
      • Ha a mezőt létrehozó Q töltéstől r távolságra elhelyezzük a próbatöltést, akkor arra erő hat.
      • Ha ugyanabba a pontba kétszer háromszor nagyobb próbatöltést helyezünk, akkor kétszer háromszor nagyobb lesz az erőhatás mértéke is.
      • Tehát a mező adott pontjában a próbatöltésre ható erő és a próbatöltés nagysága között egyenes arány van. A kettő hányados a mező adott pontját jellemzi, amelyet elektromos térerősségnek nevezünk.

      Az elektromos térerősség vektormennyiség.

      Nagysága a próbatöltésre ható erő és a próbatöltés nagyságának hányadosa.
      Iránya a pozitív próbatöltésre ható erő irányával egyezik meg.

       

       

      Pontszerű töltés elektromos térerőssége


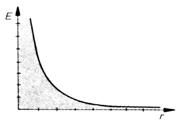
      A pontszerű töltés elektromos térerőssége egyenesen arányos a mezőt létrehozó töltés nagyságával, és fordítottan arányos a töltéstől mért távolság négyzetével.
      Az arányossági tényező: k.

       

      Szuperpozíció elve az elektrosztatikában

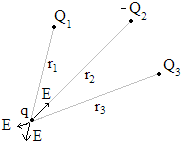
      Ha az elektromos mezőt több töltés hozza létre, akkor bármely pontba az elektromos térerősség megegyezik az egyes töltésekből származó térerősségek vektori eredőjével.

       

      Elektromos mező szemléltetése

      Az elektrosztatikus mezőt térerősség vonalak segítségével lehet szemléltetni.

      A térerősség vonalak olyan képzeletbeli és térbeli görbék, amelyeknek bármely pontjába húzott érintő iránya az adott pont térerősségnek irányába mutat, és olyan sűrűn rajzoljuk ezeket a görbéket, hogy egységnyi felületre merőlegesen annyi haladjon keresztül, amennyi az adott helyen a térerősség nagysága.

       

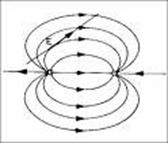
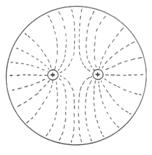
      A homogén elektromos mező minden pontjában a térerősség nagysága és iránya megegyezik. Az ilyen mezőt egyenlő hosszúságú és sűrűségű térerősség vonalakkal szemléltetjük.
    2. Fluxus fogalma
      Az elektromos mező jellemzésére szolgáló fizikai mennyiség az elektromos fluxus. Jele: Ψ

      Az elektromos fluxus megegyezik a felület és a rá merőleges elektromos térerősség szorzatával.

      Gauss tétel (Maxwell I. törvénye)

      • Azt vizsgáljuk, hogy egy pontszerű töltéstől r távolságra mekkora az elektromos térerősség.
      • Ezt kétféleképpen is felírhatjuk. Ez a két felírási mód egymással ekvivalens, ezért egyenlővé tehető.
      Mivel ekvivalensek, egyenlők egymással, ezért:
      Ψzárt felület = Ne → Elektromos forráserősség

      Gauss levezette, hogy a zárt felületnek a fluxusa csak attól függ, hogy mennyi a felületben lévő töltések algebrai összege. Zárt felület fluxusát másképpen forráserősségnek nevezzük. Jele: Ne

      Gauss tétel, Maxwell I. Törvénye:

      Zárt felület fluxusa, azaz forráserőssége megegyezik a felületben lévő töltések algebrai összegének szorosával, vagy szorosával.

      Két feladat Gauss-tételének alkalmazására

      1. Végtelen hosszú egyenes vezetőn az egységnyi hosszra jutó töltéssűrűség σ. Mennyi a vezetőtől r távolságra az elektromos térerősség?
       

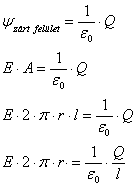
      2.  Mekkora egy A felületű vezető lemeztől r távolságra az elektromos térerősség, ha a felületi töltéssűrűség σ?
    3. Feszültség és potenciál

      Feszültség

      • Homogén elektrosztatikus mezőbe egy q próbatöltést helyezünk.
      • Miközben a mező az A-ból a B pontba juttatja a próbatöltést, munkát végez.
      • Ha a próbatöltés nagyságát kétszeresére, háromszorosára növeljük, akkor a mező által végzett munka is kétszeresére, háromszorosára nő.
      • Vagyis a mező által végzett munka és a próbatöltés között egyenesen arányosság van.

      Az elektromos mező által a mező két pontja között végzett munka és a két pont között mozgó töltés hányadosa a mező két pontjára jellemző állandót határoz meg. Ezt az állandót az A pontnak a B-hez viszonyított feszültségének nevezzük.
      A feszültség jele: U


      A fenti összefüggés csak akkor igaz, ha az elektromos mező a térerősség vonalak irányába mozdítja el a próbatöltést. Ilyenkor a térerősség vonalak irányába felvett két pont között a feszültség egyenesen arányos a két pont távolságával az arányossági tényező az elektromos térerősség.

      Potenciál

       

      Ha az elektrosztatikus mezőben tetszőlegesen kijelölünk egy nulla szintet és ehhez képest megmérjük a mező bármely pontjának feszültségét, a mező adott pontjának potenciáját kapjuk.

      Tehát a nulla szinthez képest mért feszültséget potenciálnak nevezzük.

      Két pont potenciáljának különbsége megegyezik a két pont közötti feszültséggel.

       

      Pontszerű töltés potenciálja:

      		 A pontszerű töltéstől r távolságra a potenciál
  5. Az elektrosztatikus mező tulajdonságai
    1. Az elektrosztatikus mező forrásos mező

      Az elektrosztatikus mező forrásai az elektromos töltések. A térerősség vonalak a töltésből indulnak ki és a töltéseken végződnek.

    2. Az elektrosztatikus mező konzervatív mező.

      A mező által két pont között végzett munka csak a két pont helyzetétől függ.

      Bizonyítás:

      Mekkora munkát végez az elektrosztatikus mező, amíg egy próbatöltést az A pontból a B pontba juttat?

      Nézzük ezt meg két különböző úton! Az egyik az ABC út, a másik az AB út.

      Látható, hogy a munkavégzés nagysága nem függ az útpálya hosszától.

    3. Az elektrosztatikus mező örvénymentes mező

      4. Az elektrosztatikus mezőben egy zárt görbe mentén végzett munka összege nulla.

      Bizonyítás:

       
  6. Kondenzátor és kapacitás
    1. Kondenzátor fogalma
      • A kondenzátort másképpen sűrítőnek nevezzük. Két vezetőlemezből áll, melyeknek ellentétes a töltésük.
      • Ez technikailag úgy is megvalósítható, hogy az egyik lemezt pozitív töltésűre töltjük, a másikat pedig leföldeljük. A kondenzátor vezető lemezeit fegyverzetnek is nevezzük.
      • A sűrítő elnevezés abból adódik, hogy a kondenzátor a fegyverzetek közé sűríti az elektromos mezőt, és így az elektromos térerősség vonalakat is.
    2. Kapacitás
      • Ha a kondenzátor fegyverzetén a töltésmennyiséget kétszeresére, háromszorosára növeljük, térerősség is kétszeresére, háromszorosára fog nőni.
      • Ebből viszont az is következik, hogy a fegyverzetek között a feszültség kétszeresére, háromszorosára nő. Tehát a fegyverzeteken lévő töltésmennyiség és a fegyverzetek között kialakuló feszültség között egyenes arány van. Q~U

      A kondenzátor fegyverzetein lévő töltésmennyiség és a fegyverzetek közötti feszültség hányadosa állandót határoz meg. Ez az állandó a kondenzátor töltéstároló képességére jellemző kapacitás. Jele: C

      Egy farad a kondenzátor kapacitása, ha 1V feszültség mellett 1C töltésmennyiséget képes tárolni.

      A kondenzátor kapacitása függ:

      • a fegyverzetek nagyságától,
      • azok távolságától
      • és a köztük lévő szigetelő anyagtól.

      A kondenzátor kapacitása nem függ a töltésmennyiségtől és a feszültségtől.

    3. R sugarú vezetőgömb kapacitásának meghatározása

      Vezetőgömb kapacitása csak a gömb sugarától függ.

    4. Síkkondenzátor kapacitása

      Az elektromos térerősséget Gauss-tétel segítségével így határoztuk meg:
      és ebből: 
    5. Kondenzátorok kapcsolása

      Soros kapcsolás:

      Soros kapcsolásnál elektromos megosztás miatt a fegyverzeteken megegyezik a töltésmennyiség.

      A kondenzátorok soros kapcsolásánál az eredő kapacitás reciproka megegyezik a sorba kapcsolt kapacitások reciprokának összegével.

      Párhuzamos kapcsolás:

      A kondenzátorok párhuzamos kapcsolásánál valamennyi kondenzátoron azonos a feszültség.

      Párhuzamos kapcsolásnál az eredő kapacitás megegyezik az egyes kapacitások összegével.

  7. Az elektrosztatikus mező energiája és energiasűrűsége

    Ha elektrosztatikus mezőbe töltést helyezünk, akkor a mező a töltést elmozdítja, azaz a mező munkát végez. Mivel a mező képes munkavégzésre, ezért energiával is rendelkezik.

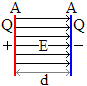
    Vizsgáljuk meg hogy mennyi munkát kell végeznünk ahhoz, hogy egy pozitív Q töltéssel ellátott A felületű lemeztől d távolságra elmozdítsunk egy hasonló méretű –Q töltésű lemezt.

    Az elektromos térerősség egy Q töltésű lemez környezetében Gauss-tétel felhasználásával határozható meg.

    A fenti képletbe, ha behelyettesítjük a térerősségre kapott összefüggést, akkor a végzett munka a következőképpen fejezhető ki:



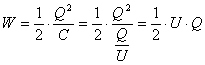
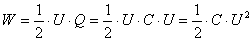    A kondenzátor fegyverzeti között a homogén elektrosztatikus mezőben tárolt energiát kiszámíthatjuk: 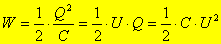 összefüggések felhasználásával.

    Elektrosztatikus mező energiájának meghatározása általános esetben

    Elektrosztatikus mező nemcsak kondenzátor fegyverzetei között alakulhat ki. Az előző összefüggés felhasználásával általánosan is kifejezhetjük a mező energiáját, energiasűrűségét.

    Az elektrosztatikus mező energiája egyenesen arányos az elektromos térerősség négyzetének és a mező térfogatának szorzatával.
    Az arányossági tényező: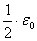  vagy .

    Elektrosztatikus mező energiasűrűsége:

    Az elektromos mező energiasűrűsége a térerősség négyzetével arányos.

  8. Vezetők elektrosztatikus mezőben
    1. Megosztás jelensége

      • Ha két elektroszkópot egy vezetőrúddal kötünk össze, akkor az elektroszkóp nem jelez töltést.
      • Ha a rendszer közelébe egy bőrrel megdörzsölt üvegrudat helyezünk, akkor mindkét elektroszkóp töltést fog jelezni.
      • A jelenség azzal magyarázható, hogy az üvegrúd által létrehozott elektromos mező kölcsönhatásba lép a vezetőrúdban lévő töltésekkel. Ennek köszönhetően az egyik elektroszkóp negatív a másik pozitív töltéstöbbletet jelez. A jelenség neve: elektromos megosztás.

      Elektromos megosztásról akkor beszélünk, ha külső elektromos mező hatására egy vezetőben töltésszétválasztódás jön létre.

    2. Megosztás következményei

      Az elektromos megosztás során a töltésszétválasztódás addig tart, amíg a vezető belsejében a külső és a belső mezőből származó elektromos térerősség nulla nem lesz.

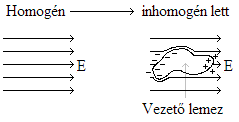
      Vezető belsejében az elektromos térerősség mindig nulla.

      Azáltal hogy egy vezetőt elektrosztatikus mezőbe helyezünk a következő változások figyelhetők meg:

      1. Létrejön az elektromos megosztás.
      2. Megváltozik az elektromos mező szerkezete.
      3. A térerősség vonalak a vezetőn merőlegesen végződnek és merőlegesen lépnek ki.
      4. A töltésszétválasztódás ellenére a vezető felülete ekvipotenciális.
  9. Többlettöltés a vezető felületén

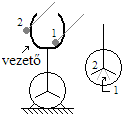
    • A kehely alakú vezetőn Q többlettöltés van.
    • Ennek a többlettöltésnek a segítségével próbálunk egy elektroszkópot feltölteni.
    • Ha a szigetelő nyélen lévő vezetőgömböt a kehely külső felületéhez érintjük, majd az elektroszkóphoz, akkor az elektroszkóp feltöltődik.
    • Ha a vezetőgömböt a kehely belső felületéhez érintjük, akkor nem tudunk többlettöltést levenni.

    A többlettöltés mindig a vezető külső felületén jelenik meg.

    (középen lyuk, oda juttatjuk a többlettöltést)

    Ha egy vezetőnek a belsőjébe többlettöltést juttatunk, az elektromos megosztás miatt, ez a többlettöltés a vezető felületén jelenik meg. A vezető belsejében, sem többlettöltés sem elektromos mező nem lehet.
    Erre jött rá Faraday, amikor sűrű fémhálóval „burkolt” körül egy embert, és a fémhálót elektrosztatikusan feltöltötte. Az embernek semmi baja nem esett.
  10. Elektromos térerősség a vezető környezetében

     

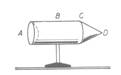
    Ha egy vezető felületére Q töltést viszünk, akkor a töltéseloszlás nem lesz egyenletes. A töltések úgy fognak eloszlani, hogy a vezető felülete ekvipiotenciális legyen. A rajzon látható vezetőnél a D pontban lesz a legnagyobb a töltéssűrűség.

     

    Minden felület egy-egy gömbbel közelíthető (egy síkfelületet végtelen nagy sugarú gömbbel tudunk helyettesíteni). Vizsgáljuk meg azt az esetet, amikor egy r1 és egy r2 sugarú vezetőgömböt vezetővel kötünk össze, és a felületükre Q töltést viszünk.
    Ezek a töltések úgy oszlanak el, hogy a két gömb felülete ekvipotenciális felület legyen.

    Ebből következik, hogy a töltések aránya megegyezik a gömbök sugarainak arányával.

    Ha a Gauss-tétel alapján számoljuk a töltések arányát, akkor

    .

    A két arányból levezethető, hogy minél kisebb egy vezető görbületi sugara (annak a képzeletbeli gömbnek a sugara, amivel közelíteni lehet a felületet), annál nagyobb a környezetében a térerősség.

     

    Elektromos szél:

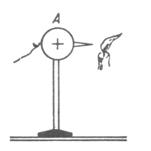
    Feltöltünk egy csúccsal ellátott vezetőgömböt. A csúcs környezetében kialakuló nagy térerősség a levegő molekuláit polarizálja. A molekulák így nekicsapódnak a csúcsnak, és attól töltést vesznek át. A csúcs az azonos töltésű molekulákat óriási kezdősebességgel taszítja el. (mert a csúcsnál nagy a térerősség).

    Ha egy csúccsal ellátott vezető gömbnek pozitív töltést adunk,  akkor hamarosan a környezetében lévő másik vezetőgömbnek is pozitív lesz a töltése.

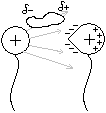
    Elektromos megosztás miatt a csúcsnak negatív lesz a töltése, és nagy lesz a környezetében a térerősség. A csúcshoz csapódó molekulák elviszik ezt a negatív töltést, így a csúccsal ellátott gömb pozitív töltésűvé válik.
  11. Szigetelők elektrosztatikus mezőben

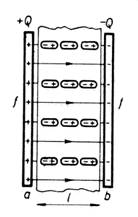
    Egy kondenzátor fegyverzetei között homogén elektrosztatikus mező van. Ha a fegyverzetek közé szigetelőt helyezünk, akkor az elektromos mező polarizálja a szigetelőben lévő molekulákat. Úgynevezett polárláncok alakulnak ki a szigetelőben. Ezáltal a fegyverzetek között a térerősség csökken, mivel a térerősség vonalak egy része a polárláncon végződik, illetve onnan indul ki. Így nő a kondenzátor kapacitása.

     

    A relatív dielektromos állandó (relatív permitivitás) az a viszonyszám, mely megmutatja, hogy az adott szigetelő jelenlétében hányszorosára nő egy kondenzátor kapacitása a vákuumbeli értékhez képest. Ez az anyagi minőségre jellemző érték.