1. Az elektromágneses indukció és annak fajtái

    A mágneses mezőben lezajló változásokkal kapcsolatos jelenségeket elektromágneses indukciónak nevezzük.

    Az indukciós jelenségeknek két típusa lehet:

    • Mozgási indukció
      Mozgási indukció körébe azok a jelenségek tartoznak, amikor a vezető mozog az állandó mágneses mezőben.
    • Nyugalmi indukció
      Nyugalmi indukció során a nyugvó vezető környezetében a mágneses mező változik.
  2. A mozgási indukció

    Homogén mágneses mezőben az indukcióvonalakra merőlegesen vezetőszálat helyezünk el. Ha a vezetőszálat a mágneses indukcióra is és a vezetőre is merőleges irányú sebességgel mozgatjuk, akkor a vezetőszál két vége között feszültség mérhető.

    A jelenség azzal magyarázható, hogy a vezetőben levő töltések a vezetőszállal együtt a mágneses indukcióvektorra merőlegesen mozognak. Így a töltésekre hat a Lorenz-erő, aminek következtében a vezető egyik vége pozitív a másik negatív töltésű lesz.

    A mágneses mezőben mozgó vezetőben a Lorenz-erő hatására létrejövő töltés- szétválasztást mozgási indukciónak nevezzük.

    A mozgási indukció hatására a töltésszétválasztódás addig tart, amíg a Lorenz-erő egyenlő nem lesz a szétválasztott töltések közötti Coulomb-erővel.



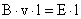
    Ha homogén mágneses mezőben az indukcióvonalakra merőleges l hosszúságú vezetőt a mágneses indukcióra is és a vezetőszálra is merőleges v sebességgel mozgatunk, akkor a vezető két vége között feszültség mérhető.

    Ez az indukált feszültség egyenesen arányos a vezető szakasz hosszának és sebességének szorzatával, az arányossági tényező a mágneses indukció.
  3. Lenz-törvény

    Az indukált feszültség által indított áram irányát Lenz-törvénye alapján állapítjuk meg.

    • Ha a vezetőszál v sebességgel megmozdul a kereten, akkor a töltésszétválasztás miatt a zárt körben áram indul meg.
    • Ennek következtében az áramjárta vezetőre olyan irányú erő fog hatni, ami csökkenteni igyekszik a sebességét.

    Az indukált feszültség mindig olyan irányú áramot indít, amelynek hatása akadályozza az őt létrehozó hatást.
    • Ha a vezetőszálat v sebességgel akarjuk mozgatni, akkor ahhoz a vezetőre állandó F erővel kell hatni.
    • Ennek az erőnek a nagysága:  ,amely a mozgás során s úton munkát végez.
    • Ez a munka megegyezik az indukált feszültség által indított áram munkájával.
    • Így az energia megmaradásából is levezethető az indukált feszültség képlete.



    A zárt alumíniumgyűrű elmozdul a mágnes elmozdulásának irányába, a nyitott alumíniumgyűrű viszont nyugalomban marad. Ez a jelenség is Lenz-törvényével magyarázható.
  4. Nyugalmi indukció

    Nyugalmi indukció során a mágneses mező változik a nyugvó vezető körül.

    • Nyugvó tekercs belsejében mozgatjuk a mágnest.
    • A középállású feszültségmérő kitérésének iránya a mozgás irányától függ.
    • Az indukált feszültség nagysága függ a mágneses mező változásának sebességétől, és annak a tekercsnek a menetszámától, amelyben a feszültség indukálódik.
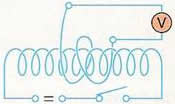
    • Az áramkör nyitásakor és zárásakor a külső tekercshez kapcsolt feszültségmérő feszültséget jelez.

    Az indukált feszültség egyenesen arányos a fluxusváltozás sebességének és a tekercs menetszámának a szorzatával, az arányossági tényező -1. (a mínusz előjel Lenz-törvényéből következik.)

    Nyugalmi indukció jelenségének magyarázata

    Az időben változó mágneses mező maga körül egy elektromos mezőt hoz létre, amely kölcsönhatásba tud lépni a vezetőben lévő nyugvó töltésekkel.

  5. Időben változó mágneses mező által keltett elektromos mező tulajdonságai

    1. Időben változó mágneses mező által keltett elektromos mező örvényes elektromos mezőt hoz létre.
    2. Ez az elektromos mező — szemben az elektrosztatikus mezővel — forrásmentes mező.
    3. Ezt bizonyítja az is, hogy az elektromos térerősség-vonalak önmagukba záródó görbék.
    4. Időben változó mágneses mezőben ha felveszünk egy zárt görbét, és ezt a görbét olyan ∆s szakaszokra bontjuk, amely mentén az elektromos térerősség nagysága állandó, majd képezzük az szorzatok összegét, eredményképpen a görbe által határolt felületen a fluxusváltozás sebességét kapjuk. Ezt Faraday, angol tudós ismerte fel, és tiszteletére Faraday-féle indukciós törvénynek nevezzük.

    5. A kialakuló elektromos mező szerkezetét a balkéz szabály segítségével szemléltetjük.

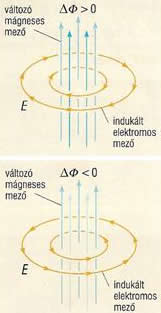
      Ha balkezünk hüvelykujja a fluxusváltozás irányába mutat, akkor a begörbített négy ujjunk az indukált elektromos mező térerősség-vonalainak görbületét mutatják.

    6. Az indukált elektromos mező nem konzervatív mező.
  6. Kölcsönös és önindukciós jelenség

    Kölcsönös indukciós jelenség

    • Kölcsönös indukció bemutatható két tekercs segítségével. A két tekercset közös vasmaggal kapcsoljuk össze.
    • Ha az első tekercsben változtatjuk az áram erősségét, akkor a második tekercsben feszültség mérhető.

    A jelenség magyarázata a következő:

    • Az első tekercsben az áramerősség változása miatt egy időben változó mágneses mező alakul ki.
    • A közös vasmag miatt ez a változás a második tekercsben is fennáll.
    • A mágneses mező változása egy örvényes elektromos mezőt indukál, ami kölcsönhatásba lép a második tekercsben lévő elektronokkal.

    A kölcsönös indukció során az indukált feszültség egyenesen arányos az áramerősség-változás sebességével, az arányossági tényező a kölcsönös indukciós együttható mínusz egyszerese.

    ,
    ahol L12 a kölcsönös indukciós együttható.

    Egy henry egy rendszer kölcsönös indukciós együtthatója, hogyha az egyik vezetőben egy másodperc alatt bekövetkező egy amper áramerősség-változás a másik vezetőben egy volt feszültséget indukál.

    Kölcsönös indukciós együttható levezetése

    Önindukció

    • Az áramkörbe két teljesen azonos teljesítményű izzót kapcsolunk.
    • A változtatható ellenállásra azért van szükség, hogyha az áramkör tartósan zárva van, akkor mindkét izzó azonos fényerősséggel világítson.
    • Az áramkör zárásakor az egyes izzó később kezd el teljes fényerővel világítani.
    • A jelenség magyarázata:
      • A kapcsoló zárásakor az áramerősség nagysága a tekercsben a nullához képest folyamatosan nő.
      • Így a tekercs belsejében egy időben változó mágneses tér alakul ki. Ez egy örvényes elektromos mezőt hoz létre, amely által indított áram akadályozza az áram növekedését (Lenz-törvény).
    • Az áramkör nyitásakor az egyes izzó később alszik el, mint a kettes.
      • Az áram csökkenése a tekercsben, időben változó mágneses teret eredményez.
      • Ez egy olyan feszültséget indukál, amely által indított áram akadályozza az áramerősség csökkenését.

    Az önindukció során a tekercsben indukált feszültség egyenesen arányos az áramváltozás sebességével, az arányossági tényező az önindukciós együttható mínusz egyszerese.

    ,
    ahol L a tekercs önindukciós együtthatója.

    Önindukciós együttható levezetése

  7. Elektromos mező energiája

    Egy tekercs belsejében a mágneses mezőnek a kiépülése, illetve megszüntetése nem pillanatszerű folyamat. Ez azt jelenti, hogy a mágneses mező tehetetlenséggel rendelkezik, amiből következik, hogy energiájuk is van.

    Kísérlet

    Amikor a kapcsolót az egyes állásból a kettesbe átkapcsoljuk, akkor az izzó felvillan. Az átkapcsolás pillanatában elkezd csökkenni a tekercs belsejében a mágneses mező. Ez a fluxusváltozás egy feszültséget indukál, amely által keltett áram a korábbi állapotot igyekszik fenntartani.
    Az indukált áram által végzett munka a tekercs belsejében lévő mágneses mező energiájával egyezik meg.

    Az indukált áram munkája

    Az összegzést egyszerű matematikai eljárással végezhetjük el. Ha ábrázoljuk az áramerősség függvényében az L∙I szorzatot, akkor egy egyenes arányt kifejező grafikont kapunk. Ha kijelölünk kicsi ∆I szakaszt, akkor a hozzá tartozó terület közelítőleg ∆I∙L∙I. Ezen kicsi területeknek az összege adja a grafikon alatti területet, ami a munkával egyezik meg.

    Így:

    Az áramjárta tekercs belsejében kialakuló mágneses mező energiája egyenesen arányos az áramerősség négyzetével, az arányossági tényező az önindukciós együttható fele.

    Mágneses mező energiája általánosan

    A mágneses mező energiája egyenesen arányos a mező térfogatának és a mágneses indukció négyzetének a szorzatával, az arányossági tényező az .

    Mágneses mező energiasűrűsége