- A geometriai optika tárgya
A fénytan (optika) a fényjelenségekkel és a fény terjedési törvényeivel foglalkozik.
A geometriai optika egyszerű modell, amely a fény terjedését a fényforrásból minden irányba kilépő fénysugarakkal írja le, és nem foglalkozik a fény természetével (hullám vagy részecske).
Alapfeltevései a következők:
- a fénysugár homogén közegben egyenes vonalban terjed,
- új közeg határfelületén megtörik és/vagy visszaverődik,
- a fénysugár útja megfordítható.
A geometriai optika modellje jól alkalmazható az optikai leképezésnél
- Geometriai optikában használatos alapfogalmak
- Fényforrások és csoportosításuk
Környezetünkről nagyon sok információt a látás útján, a fény segítségével szerzünk. Szemünkbe a fény kétféle úton juthat:
- közvetlenül a fényt kibocsátó testről,
- más testekről való visszaverődés útján.
Ez a fényforrások csoportosításának egyik alapja.
Elsődleges fényforrás: az olyan fényforrás, amely saját maga bocsátja ki a fényt.
Ilyen például: Nap, csillagok, gyertya, izzólámpa.Másodlagos fényforrás: ezek olyan fényforrások, amelyek csak a ráeső fény
visszaverődése miatt láthatók.
Ilyen például: Hold, asztal, könyv.A fényforrásokat méretük alapján is szokták csoportosítani.
Pontszerű fényforrások: A fényforrás mérete a vizsgált jelenségnél fellépő méretekhez képest elhanyagolható. Kiterjedt fényforrás: A fényforrás mérete nem elhanyagolható. - Fénysugár

Az igen vékony párhuzamos fénynyalábot fénysugárnak nevezzük.
Ennek kísérleti előállítása a következőképpen történhet:- Egy üvegkádba füstöt fújunk, majd a kádat üveglappal lefedjük.
- A kád elé egy erős fényű izzólámpát helyezünk.
- Ennek fénye egy kartonlapon lévő nyíláson keresztül juthat be az üvegkádba.
- Ha a lámpát távolítjuk, akkor a fénykúp nyílásszöge csökken. Így juthatunk el a geometriailag egyenessel ábrázolható fénysugárhoz.
- Árnyék, félárnyék
A fény egyenes vonalú terjedésének a következménye az árnyékjelenség.
Árnyék

Ha egy pontszerű fényforrás és az ernyő közé egy átlátszatlan tárgyat helyezünk, akkor az ernyőn kirajzolódik a test éles árnyéka.
Az árnyéktérbe a fényforrásból egyetlen egy fénysugár sem érkezik.Félárnyék

Ha a pontszerű fényforrást kiterjedt fényforrásra cseréljük, akkor az árnyék határa elmosódik, szélén fokozatosan világosodik.
Lesz az árnyéktérnek olyan része, amelyet a fényforrásnak csak bizonyos részei világítanak meg. Ez a félárn
- Fényforrások és csoportosításuk
- A fény terjedési sebességének meghatározása
A fény terjedéséhez időre van szükség. Ezt már Galilei is sejtette, de először Olaf Römer, dán csillagász 1685-ben határozta meg a fény terjedési sebességét. Méréséhez csillagászati távolságokat használt.

Olaf Römer a Jupiter Io holdjának holdfogyatkozását vizsgálta. Észrevette, hogy a holdfogyatkozás időtartama nem állandó, hanem periodikusan változik.
Megfigyelte, hogy a fogyatkozás akkor volt rövidebb, ha a Jupiter és a Föld a Nap ugyanazon az oldalán volt (A), és akkor volt a leghosszabb, ha két bolygó az ellentétes oldalon állt (C).
A megfigyelést azzal hozta kapcsolatba, hogy a fénynek különböző utakat kell befutni a Jupiter és a Föld között, és e helyes feltevés alapján kiszámította, hogy a fény a földpálya átmérőjének megfelelő hosszúságú utat 16 perc alatt teszi meg.
A XII. sz. órái nem voltak valami megbízhatóak, és a földpálya átmérőjét sem ismerték elég pontosan, így Römer 2.108 m/s sebességértéke lényegesen kisebb, mint a ma ismert érték.
Később a fénysebesség mérésére más módszereket is kidolgoztak (Fizeau, Foucault, Michelson).
A fény terjedési sebessége légüres térben
 .
. - A fény viselkedése két közeg határán

Új közeg határához érkezve a fény részben elnyelődik, részben visszaverődik, részben megtörik.
A jelenség megfigyelhető, ha egy fluoreszceinoldattal töltött üvegkád fölé füstöt fújunk, majd a két közeg határfelületét párhuzamos fénynyalábbal világítjuk meg. A fény terjedési iránya megváltozik.
Nézzük az egyes jelenségeket külön-külön!- A fény elnyelődése
A fény új közeg határfelületéhez érkezve energiájának egy részét átadja az új közegnek. Ezt a jelenséget szoktuk úgy nevezni, hogy a fény elnyelődik.
- A fény visszaverődése

Az ábra a sík felületre érkező fénysugár visszaverődését mutatja.
A következő elnevezéséket használjuk:
- beeső fénysugár (s): a felülethez tartó fénysugár,
- visszavert fénysugár (s'):a felülettől távolodó fénysugár,
- beesési pont (O): ahol a beeső fénysugár a felületet éri,
- beesési merőleges (n): a beesési pontban a felületre állított merőleges,
- beesési szög (α): a beeső fénysugárnak a beesési merőlegessel bezárt szöge,
- visszaverődési szög (α'): a visszavert fénysugárnak a beesési merőlegessel bezárt szöge.
Fényvisszaverődés törvényei:
- A beeső fénysugár, a beesési merőleges és a visszavert vénysugár egy síkban van.
- A visszaverődési szög egyenlő a beesési szöggel.
Ezt a törvényt Euklidesz már i.e. 300 körül megállapította.
Ha párhuzamos fénynyaláb tökéletesen sima felülethez érkezik, akkor a visszavert fénynyaláb is párhuzamos lesz.

Ha a visszaverő felület érdes, akkor a visszavert fénysugarakszétszóródnak, mivel a beesési merőlegesek nem lesznek párhuzamosak. Ezt a jelenséget nevezzük diffúz fényvisszaverődésnek.

- A fény törése
Fény törése akkor következik be, ha a fény olyan új közeghez érkezik, amelyben más a terjedési sebessége. Ilyenkor legtöbbször a terjedési iránya is megváltozik.
Az elnevezések hasonlóak a visszaverődésnél megismertekkel, csak visszavert fénysugár helyett megtört fénysugár, visszaverődési szög helyett törési szög szerepel.


A fénytörés jelensége az optikai-korong (Hartl-korong) segítségével jól megfigyelhető.
A jelenség megfigyelése szempontjából fontos, hogy a forgatható optikai korong és az üveg félkorong középpontja egybe essen. Így az üveg félkorongból kilépő fénysugár irányváltoztatás nélkül halad tovább.
A kísérlet alapján megfogalmazható a fénytörés törvénye:
Fénytörés törvényei:
- A beeső fénysugár, a beesési merőleges és a megtört fénysugár egy síkban vannak.
- A beesési és a törési szög szinuszainak a hányadosa megegyezik az egyes közegekben mérhető terjedési sebességek hányadosával. Ez a hányados a második közegnek az első közeghez viszonyított törésmutatójával egyenlő.

Ezt a törvényt törési törvénynek vagy Snellius-Descartes-törvénynek nevezzük.
Megfigyelhető, hogy a felületre merőlegesen érkező fénysugár irányváltoztatás nélkül halad tovább.
Valamely anyagnak légüres térre vonatkoztatott törésmutatóját abszolút törésmutatónak nevezzük.
Két közeg közül az az optikailag sűrűbb közeg, amelynek abszolút törésmutatója nagyobb.
- A fény teljes visszaverődése
Ez a jelenség akkor következik be, ha a fény az optikailag sűrűbb közeg felől a ritkább felé halad.

Ilyenkor a törési szög nagyobb, mint a beesési szög.
Ilyenkor a beesési szöget növelve elérhető egy olyan érték, amelyhez 90°-os törési szög tartozik (2-es fénysugár).
Azt a beesési szöget, amelyhez 90°-os törési szög tartozik, a teljes visszaverődés határszögének (αh) nevezzük.


- Plánparalel lemez fénytörése
Két párhuzamos síkkal határolt átlátszó testet plánparalel lemeznek nevezünk.
A ferdén beeső fénysugarat a plánparalel lemez önmagával párhuzamosan eltolja.
A felületre merőlegesen eső fénysugár eltolódása természetesen nulla.


A vastag kirakatüvegen keresztül szemlélve a tárgyakat a valóságosnál közelebb látjuk.
(A pont helyett az A'-ben) - Prizma fénytörése
Egymással szöget bezáró síklapokkal határolt átlátszó test a prizma. A síklapok által bezárt szöget a prizma törőszögének nevezzük (φ).
Az ábrán látható a fénysugár útja a prizmában.
- Fénytörés a természetben

A vizek mélysége a valóságosnál kisebbnek tűnik, mert a fenék A pontjából kiinduló, szemünkbe jutó fénysugár visszafelé történő meghosszabbításai, a fénytörés miatt a felszínhez közelebb A' pontban metszik egymást, s mi úgy látjuk, mintha onnan indulnának ki.
A vízbe merülő tárgyak, pl. a teáskanál a felszínnél megtörni látszanak, mert az A pontból a szemünkbe jutó fénysugár visszafelé történő meghosszabbításainak metszéspontja A' pont.

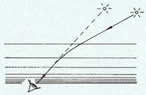
A légkör nem homogén, felfelé ritkul, ezért törésmutatója csökken. Ezért az égitestekről a légkörön át ferdén a szemünkbe jutó fénysugár nem egyenes, hanem a folytonos fénytörés miatt görbe vonal. Mi a szemünkbe érkező fény irányában, azaz a görbe érintőjének az irányában, a valóságosnál magasabban látjuk az égitesteket.
A tűzhely, a kályha és nyári melegben a föld felett a felszálló meleg légáramlatban rendszertelenül változik a sűrűség, és így a törésmutató is. Az ilyen légrétegen át nézett tárgyak reszketni látszanak a szüntelenül változó fénytörés miatt.
Délibáb

Erős napsütésben a talaj feletti levegőréteg ritkább lehet a felette lévőnél, és így teljes visszaverődés áll elő. Ennek köszönhető, hogy a tárgyaknak a fordított állású képét látjuk.
Ugyanezért látjuk meleg nyári napsütésben, autóban ülve az út távolabbi foltjait tükrösen csillogni. Ilyenkor az égboltról ferdén érkező fénysugarak szenvednek teljes visszaverődést.Fata morgana
Ahol messze ellátni (pl. a tengeren), az elég nagy beesési szöggel induló fénysugarak a felső ritkább rétegekről visszaverődve a szemünkbe juthatnak. Ezek meghosszabbításában a távoli tárgyak fordított állású képét látjuk.
- A fény elnyelődése
- Leképezés tükrökkel
- Síktükörrel

Ha élethű képet akarunk látni magunkról, akkor síktükörbe nézünk.
A síktükör által alkotott kép jellemzői:
- a kép egyenes állású,
- látszólagos,
- a képtávolság megegyezik a tárgytávolsággal,
- a képnagyság megegyezik a tárgynagysággal,
- a jobb és a bal oldal felcserélődik.
Látszólagos kép akkor keletkezik, ha
- egy tárgy pontjairól kiinduló fénysugarak valamely optikai eszköz hatására úgy tartanak szét, mintha a tér egy pontjából indultak volna ki.
- Az ilyen kép ernyőn nem fogható fel.
- Az emberi tudat a szembe érkező széttartó fénysugarak metszéspontjában képzeli el a képpontot.
- A gömbtükör jellemzői

A gömbtükör egy olyan gömbhéjszelet, amelynek vagy a külső vagy a belső felülete tükröz.
A gömbhéjszelet szimmetriatengelyét optikai tengelynek nevezzük.
Az optikai tengely és a gömbszelet közös pontja az optikai középpont (O).
A gömb középpontját geometriai középpontnak nevezzük (G).
A gömb sugara a görbületi sugár (r).
A gömbtükör nyílásszöge φ. Ha a nyílásszög kisebb, mint 5°, akkor kis nyílásszögű gömbtükörről beszélünk. A továbbiakban csak ezek leképezését vizsgáljuk.

Az optikai tengellyel párhuzamos fénysugarak az optikai tengely egy pontjában, a fókuszpontban (F) metszik egymást.
A fókuszpont és az optikai középpont távolsága a fókusztávolság (f)
Belátható, hogy a fókusztávolság a görbületi sugár fele.


- Homorú gömbtükörrel
Ha egy gömbtükör belső felülete tükröz, akkor beszélünk homorú gömbtükörről.
A homorú gömbtükör nevezetes sugarai:

- Az optikai tengellyel párhuzamosan beeső fénysugár visszaverődés után a gyújtóponton halad át.
- A gyújtóponton át beeső fénysugár az optikai tengellyel párhuzamosan verődik vissza.
- Az optikai tengely mentén beeső fénysugár önmagában verődik vissza.
- Az optikai középpontba beeső fénysugár az optikai tengelyre szimmetrikusan verődik vissza.
Az optikai tengellyel nem párhuzamos sugarakat is egy pontba gyűjti a homorú tükör. Ez a pont az optikai tengelyre, a fókuszba állított merőleges síkon van. Ez a fókuszsík.

Homorú gömbtükör képalkotása

Ha a tárgy a geometriai középponton kívül van, akkor a kép a fókuszpont és a geometriai középpont között keletkezik.
A kép:
- valódi,
- fordított állású és
- kicsinyítet.
Nevezetes sugarak segítségével bármely tárgyhelyzetben könnyen megszerkeszthető a homorú gömbtükör által alkotott kép.

Ha a tárgy a geometriai középpontban van, akkor a kép is a geometriai középpontban keletkezik.
A kép:
- valódi,
- fordított állású és
- nagyítása 1.

Ha a tárgy a fókuszpont és a geometriai középpont között van, akkor a kép a geometriai középponton kívül keletkezik.
A kép:
- valódi,
- fordított állású és
- nagyított.

A fókuszpontban lévő tárgyról a homorú gömbtükör nem alkot képet.

Ha a tárgy a fókuszponton belül van akkor a homorú gömbtükör
- nagyított,
- egyenes állású és
- virtuális képet alkot.
- Domború gömbtükörrel
Ha egy gömbtükör külső felülete tükröz, akkor beszélünk domború gömbtükörről.
A domború gömbtükör nevezetes sugarai:
- Az optikai tengellyel párhuzamosan beeső fénysugár visszaverődés után úgy halad, mintha a tükör mögötti fókuszpontból indult volna ki.
- A tükör mögötti gyújtópont felé beeső fénysugár az optikai tengellyel párhuzamosan verődik vissza.
- A geometriai középpont felé beeső fénysugár önmagában verődik vissza.
- Az optikai középpontba beeső fénysugár az optikai tengelyre szimmetrikusan verődik vissza.
Az egymással párhuzamos, de az optikai tengellyel nem párhuzamos sugarakat a domború gömbtükör úgy szórja szét, hogy a visszavert fénysugarak meghosszabbítása a tükör mögött egy pontban metszik egymást. Ez a pont az optikai tengelyre, a fókuszba állított merőleges síkon van. Ez a fókuszsík.

A domború gömbtükör képalkotása

A domború gömbtükör bármely tárgyhelyzetben
- virtuális,
- egyenes állású
- kicsinyített képet alkot.
- Gömbtükrök nagyítása
A nagyítás a képnagyság és a tárgynagyság hányadosa. Jele: N



Mind homorú, mind domború gömbtükörnél ABO háromszög hasonló az A'B'O háromszöghöz. Így a nagyítás:

- GömbLeképezési törvény
Gömbtükröknél a tárgytávolság, a képtávolság és a fókusztávolság közötti kapcsolatot a leképezési törvénnyel fejezhetjük ki.
A leképezési törvény levezetése

Az A'B'O háromszög hasonló az ABO háromszöghöz. Ezért az oldalak aránya megegyezik:
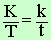
Az ábrán felfedezhető két másik hasonló háromszög is. Az LHF háromszög hasonló A'B'F háromszöghöz. Mivel a gömbtükör kis nyílásszögű, ezért az

Így a két hasonló háromszög oldalainak aránya:

A két egyenlet bal oldala megegyezik, tehát a jobb oldalak is egyenlők.

Az egyenletet átrendezve megkapjuk a leképezési törvényt:

Gömbtükrök fókusztávolságának reciproka megegyezik a tárgytávolság és a képtávolság reciprokának összegével.
Leképezési törvény alkalmazásának feltétele gömbtükrök esetén:
- Homorú gömbtükör esetén a görbületi sugár és a fókusztávolság előjele pozitív.
- Domború gömbtükör esetén a görbületi sugár és a fókusztávolság előjele negatív.
- Valódi kép esetén a képtávolság és a képnagyság előjele pozitív.
- Látszólagos kép esetén a képtávolság és a képnagyság előjele negatív.
- Síktükörrel
- Leképezés optikai lencsékkel
- Optikai lencsék jellemzői
Az optikai lencsék gömbfelület-darabokkal, esetleg egyik oldalán síkkal határolt átlátszó testek.
Alakjuk szerint a lencsék lehetnek:

- Kétszer domború lencse (bikonvex lencse)
- Sík-domború lencse (plán-konvex lencse)
- Homorú-domború lencse (konkáv-konvex lencse)
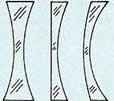
- Kétszer homorú lencse (bikonkáv lencse)
- Sík-homorú lencse (plán-konkáv lencse)
- Domború-homorú lencse (konvex-konkáv lencse)

A lencse szimmetriatengelyét optikai tengelynek, az optikai tengely döféspontját optikai középpontnak nevezzük.
A továbbiakban olyan lencsékkel foglalkozunk, amelyek vastagsága elhanyagolható az átmérőjükhöz képest. Az ilyen lencséket vékony lencséknek nevezzük.
A továbbiakban csak a vékony lencsékkel foglalkozunk.A lencsén a fénysugár általában kétszer megtörve halad át. A fénysugár útját a fénytörés törvénye szerint szerkeszthetjük meg. A beesési merőleges a felülethez tartozó sugár.
Gyűjtőlencse


- Gyűjtőlencsének nevezzük azt a lencsét, amely az optikai tengellyel párhuzamosan érkező fénysugarakat a lencse másik oldalán egy pontban gyűjti össze.
- Ezt a pontot a lencse fókuszpontjának (F) nevezzük.
- Minden lencsének két fókuszpontja van, amelyek a lencse két oldalán az optikai középponttól azonos távolságra helyezkednek el.
A gyűjtőlencse nevezetes sugarai

- Az optikai tengellyel párhuzamos fénysugarak kétszeres törés után a túloldali fókuszon haladnak át.
- A fókuszponton át beeső fénysugár kétszeres törés után az optikai tengellyel párhuzamosan halad.
- Az optikai középpontba beeső fénysugár irányváltoztatás nélkül halad tovább.

Az optikai tengellyel nem, de egymással párhuzamos fénysugarak is egy pontban metszik egymást. Ez a pont az optikai tengelyre merőlegesen, a fókuszba állított síkon, a fókuszsíkon van.
Szórólencse


- Szórólencsének nevezzük az olyan lencsét, amely az optikai tengellyel párhuzamosan érkező fénysugarakat kétszeres törés után úgy szórja szét, mintha azok a lencse előtti egyetlen pontból indultak volna ki.
- Ezt a pontot a szórólencse fókuszpontjának (F) nevezzük.
- A szórólencsének is két fókuszpontja van, amelyek az optikai középponthoz képest szimmetrikusan helyezkednek el az optikai tengelyen.
A szórólencse nevezetes sugarai

- Az optikai tengellyel párhuzamosan haladó fénysugár kétszeres törés után úgy halad tovább, mintha a lencse előtti fókuszpontból indult volna ki.
- Az optikai középpontba beeső fénysugár irányváltoztatás nélkül halad tovább.
- A lencse utáni fókuszpont felé beeső fénysugár kétszeres törés után az optikai tengellyel párhuzamosan halad tovább.
Lencse fókusztávolsága


Vékony lencsék fókusztávolsága függ:
- a határoló felületek görbületi sugarától és a
- lencse anyagának a közegre vonatkoztatott törésmutatójától.
A fókusztávolság kiszámítása a következőképpen történik:

Ha a felület a közeg felől nézve domború, akkor a neki megfelelő sugár pozitív.
Ha a felület a közeg felől nézve homorú, akkor a neki megfelelő sugár negatív.A méterben kifejezett fókusztávolság reciproka a dioptria. Jele: D

Megjegyzés:
- Gyűjtőlencse fókusztávolsága és dioptriája pozitív.
- Szórólencse fókusztávolsága és dioptriája negatív.
- Gyűjtőlencse képalkotása

Ha a tárgy a kétszeres fókusztávolságon kívül helyezkedik el, akkor a kép a lencse túlsó oldalán az egyszeres és a kétszeres fókusztávolság között keletkezik.
A kép:
- valódi,
- fordított állású és
- kicsinyített.
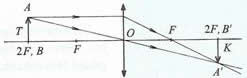
Ha a tárgy a kétszeres fókusztávolságban van, akkor a kép a lencse másik oldalán is a kétszeres fókusztávolságban keletkezik.
A kép:
- valódi,
- fordított állású,
- nagyítása 1.

Ha a tárgy az egyszeres és a kétszeres fókusztávolság között van, akkor a kép a lencse másik oldalán a kétszeres fókusztávolságon kívül keletkezik.
A kép:
- valódi,
- fordított állású és
- nagyított.

Ha a tárgy a fókuszban helyezkedik el, akkor nem keletkezik kép.

Ha a tárgy a fókuszponton belül helyezkedik el, akkor a keletkező kép ernyőn nem fogható fel, tehát
- virtuális,
- egyenes állású és
- nagyított.
- Szórólencse képalkotása

A szórólencse bármely tárgyhelyzetben
- virtuális,
- egyenes állású és
- kicsinyített képet alkot.
- Lencsék nagyítása
A nagyítás a képnagyság és a tárgynagyság hányadosa. Jele: N



Mind gyűjő-, mind szórólencse esetén az ABO háromszög hasonló az A'B'O háromszöghöz. Így a nagyítás:
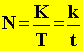
- A leképezési törvény
Lencséknél a tárgytávolság, a képtávolság és a fókusztávolság közötti kapcsolatot a leképezési törvénnyel fejezhetjük ki.
A leképezési törvény levezetése

Az A'B'O háromszög hasonló az ABO háromszöghöz. Ezért az oldalak aránya megegyezik:

Az ábrán felfedezhető két másik hasonló háromszög is. Az LOF2 háromszög hasonló A'B'F2 háromszöghöz.
Így a két hasonló háromszög oldalainak aránya:
A két egyenlet bal oldala megegyezik, tehát a jobb oldalak is egyenlők.

Az egyenletet átrendezve megkapjuk a leképezési törvényt:

Lencsék fókusztávolságának reciproka megegyezik a tárgytávolság és a képtávolság reciprokának összegével.
Leképezési törvény alkalmazásának feltétele lencsék esetén:
- Valódi kép esetén a képtávolság és a képnagyság előjele pozitív.
- Látszólagos kép esetén a képtávolság és a képnagyság előjele negatív.
- Optikai lencsék jellemzői
- Optikai eszközök
- Tükrök
- Visszapillantó tükör
Domború gömbtükör. Kicsinyített egyenes állású képet ad.
- Borotválkozó-tükör
Homorú gömbtükör, amely a fókusztávolságon belüli tárgyakról nagyított, egyenes állású látszólagos képet ad.
- Reflektorokban lévő tükör
Homorú gömbtükör, amelynek fókuszpontján helyezik el a reflektor lámpáját.
- Periszkóp

Két egymással párhuzamosan elhelyezett síktükör teszi lehetővé, hogy az akadály mögé lássunk.
- Visszapillantó tükör
- Lencse felhasználásával készítet optikai eszközök
Látószög:
Különböző távolságban lévő tárgyak látószöge.

A tárgy szélső pontjairól a szemünkbe érkező fénysugarak által bezárt szög.A tárgyaknak csak azokat a részleteit látjuk tisztán, amelynek látószöge nagyobb, mint 1 ívperc.
- Lupé


A látószög nagyítására gyűjtőlencse használható.
Ha a tárgy a fókuszon belül van, akkor a virtuális kép a tiszta látótávolságban keletkezik. Ezt látjuk.Az optikai eszköz jellemzője a szögnagyítás.
N=b/aSzögnagyítás: az optikai eszközzel és szabad szemmel észlelt látószög hányadosa.
- Fénymikroszkóp

Két gyűjtőlencséből áll:
- Tárgylencse (objektív)
- Szemlencse (okulár)
A keletkezett kép:
- nagyított,
- fordított állású,
- virtuális
- szögnagyítása kb. 2000-szeres.
- Távcsövek
A távcsövek a messze lévő tárgyak látószögét növelik.

Kepler-féle távcső
- A tárgylencse és a szemlencse fókuszpontjai egybeesnek. Így a szemünkbe majdnem párhuzamos fénynyaláb érkezik.
- A látszólagos kép nagyított lesz, amely a szemünktől nagyon messze keletkezik. A kép fordított állású.
A Kepler-távcső földi megfigyelésre nem vehető igénybe, mivel a bal és a jobb is felcserélődik.
Galilei-féle távcső

- A tárgylencse gyűjtőlencse, a szemlencse szórólencse.
- A szórólencse szem felüli fókusza egybeesik a tárgylencse fókuszával.
- Így a szembe közel párhuzamos fénynyaláb érkezik.
- A kép a szemtől messze keletkezik, és egyenes állású, virtuális lesz.
Tükrös távcső
- Nagy távolságról párhuzamosan érkező fénysugarak egy homorú gömbtükörre esnek.
- Mielőtt a fénysugarak a fókuszpontban összegyűlnének, egy 450-os szögben elhelyezett síktükör gyűjtőlencsére irányítja azokat. A síktükör csak a fénysugár irányát változtatja meg.
- A gyűjtőlencsét úgy helyezik el, hogy fókuszpontja egybeessen azzal a ponttal, ahová kétszeres visszaverődés után a fénysugarak összegyűlnek.
- Így a szemünkbe párhuzamos fénysugarak érkeznek.

- Fényképezőgép
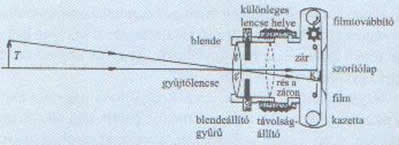
- A tárgyról a gyűjtőlencse fordított állású, valódi képet hoz létre a filmen.
- A filmre érkező fény indítja el a kémiai reakciót.
- A távolságállító lencsével állítható a mélységélesség.
- A mélységélesség azt fejezi ki, hogy adott képtávolság esetén mekkora az a tárgytávolság-tartomány, amelyről éles kép készíthető.
- Diavetítő

- A diát hátulról megvilágítják. A homorú gömbtükör az ellenkező irányba induló fénysugarakat is visszaveri.
- Egy gyűjtőlencse-rendszer összegyűjti a fénysugarakat, és a tárgyra irányítja. A diát közvetlenül a lencserendszer elé helyezzük. Így a teljes fénynyaláb kihasználható.
- A vetítőlencsét oda kell helyezni, ahol a fénynyaláb a legkeskenyebb.
- Az emberi szem

A szem átmérője kb. 24 mm.
Fénytörő részei:
- Szaruhártya (n=1,376)
- Csarnokvíz (n=1,336)
- Szemlencse (n=1,4)
- Üvegtest (n=1,336)
A négy közeg törőképessége: 50-70 dioptria.
A négy közeg a tárgy képét az ideghártyán, azaz a retinán hozza létre.

A sárgafolt a retina legérzékenyebb része. Itt található a legtöbb látóideg.
Különböző rostok, izmok szabályozzák a szemlencse domborulatát. Ezért vagyunk képesek közeli és távoli tárgyakat is élesen látni. A pupilla szabályozza a szembe jutó fény erősségét.
A térlátás annak köszönhető, hogy a két szem látótere átfedi egymást, de az agy végzi a két kép összeolvasztását.RÖVIDLÁTÁS

A közeli pontok képe éles.
A távoli pontok képe életlen.Oka:
A szemgolyó túl hosszú.
A párhuzamos fénysugarak a retina előtt metszik egymást.Javítás: szórólencsével..
TÁVOLLÁTÁS

A távoli tárgyak élesek, ha a szemünket összeszűkítjük.
Oka:
A szemgolyó túl rövid.
A távolból érkező párhuzamos fénysugarak a retina mögött metszenék egymást.Javítás: gyűjtőlencsével.
- Lupé
- Tükrök