- Bevezetés
Ha végig gondoljuk a fizika fejlődésének történetét, észrevehetjük, hogy az három nagy korszakra bontható:
- az ókori naiv természetelméletre,
- a középkori és újkori klasszikus fizikára, valamint
- a múlt századi modern fizikára.
De mit takar ez a kifejezés, hogy modern fizika?
A XIX. század végén, amikor az ismeretek áradata már óriási folyammá dagadt, akadtak fizikusok, akik azt hirdették, most már "mindenre" megtaláltuk a magyarázatot, a fizikai ismeretek lenyűgöző fellegvára szilárdan áll, és a betetőzést a Newton-féle mechanika és a Maxwell-féle egyenletek jelentik.
Más fizikusok viszont bizonyosak voltak abban, hogy az ember nem képes a "mindent" felkutatni, csak egyre többet megismerni, és tovább kutattak. Az eredmény nem maradt el: újabb nyitott kérdéseket és ellentmondásokat tártak fel a kutatók. Ezek egy részére a XX. században sikerült választ találni.
A múlt század elején a fizikai világképünkben két forradalmi átalakulás is bekövetkezett.
- Az egyik teljesen megváltoztatta az anyag és a sugárzás természetéről kialakított szemléletünket, és olyan képet festett a valóságról, amelyben a részecskék hullámként, a hullámok részecskeként viselkednek. Ekkora már a technika szakemberei is egyre tökéletesebb, finomabb és érzékenyebb eszközöket készítettek a fizikusok kísérleteihez. Így lehetővé vált az anyag belső szerkezetének egyre pontosabb megismerése.
- A másik forradalom feje tetejére állította a térről és az időről alkotott fogalmainkat. Az évek során az első forradalmat kvantumelmélet kifejezéssel illettük, a másodikat a relativitáselmélet kifejezéssel határoltuk körül.
De ne felejtsük el, amit ma modern fizikának mondunk, az holnap már klasszikussá válik, és mindig lesznek újabb és újabb megoldatlan problémák.
Ilyen volt az anyag belső szerkezetének problémája, az atom, atommag felépítése, a fény természetének magyarázata vagy a relativitáselmélet. Ezekre találta meg a választ a XX. századi fizikus társadalom.
- Az atomfogalom kialakulásának történeti áttekintése
Ma már mindenki számára természetes az atom létezése. De …
- hogyan keletkezett ez a fogalom,
- mit értettek rajta az ókorban,
- hogyan fejlődött később,
- miért csak a kvantummechanika töltötte meg reális tartalommal ezt a fogalmat?
A fejezet tanulmányozása során ezekre a kérdésekre kapunk választ.
Általános felfogás, hogy az atom fogalmát Démokritosz alakította ki már az ókorban.
Spek ulatív úton jutott el felismeréséhez. Arra gondolt, ha az anyagot daraboljuk, akkor előbb-utóbb eljutunk egy olyan részecskéhez, amely- tovább már nem osztható,
- nem hordozza az eredeti anyag tulajdonságát.
Ezt a tovább már nem osztható részecskét nevezte el a filozófus atomnak.
Az atomokról még a következő elképzelése volt:
- az atomok nagyságukat és mennyiségüket tekintve megszámlálhatatlanok,
- az űrben mozognak, ütköznek, és így jönnek létre a bonyolultabb dolgok, mint például a négy őselem: tűz, víz, levegő és föld.
Démokritosz filozófiai elgondolását követően az atomelmélet 2000 éven keresztül csak egy elképzelt hipotézis volt.
Igazán hatásosan először a kémia segítette az atomelmélet kialakulását a XVII. és a XIX. században tett felfedezéseivel. Ezek közül a legfontosabbak:
- Robert Boyle javasolta először, hogy a kémikusok feladata az, hogy megállapítsák, hogy milyen elemi testekre bonthatók az anyagok.
- Lavoisier már tisztázta az elem fogalmát. (Az azonos atomokból álló anyagot elemnek nevezzük. Két atom akkor azonos, ha bennük a protonok száma megegyezik.)
- Proust kimondta az állandó súlyviszonyok törvényét.
Vegyületekben az elemek aránya állandó. - Dalton megfogalmazta a többszörös súlyviszonyok törvényét. Atomsúly táblázatot is készített.
Ha két elem többféle arányban is képes egymással vegyülni, akkor az egyik elem azon mennyiségei, amelyek a másik elem egy adott mennyiségével vegyülnek, úgy aránylanak egymáshoz, mint a kis egész számok.
A gázokra vonatkozó törvényeket, amely csak akkor igaz, ha feltételezzük, hogy az anyag pici, szinte pontszerű "golyókból" áll, Boyle, Mariotte, Gay-Lussac és Avogadro fogalmazták meg.
(Avogadro-törvénye: Különböző gázok azonos hőmérsékleten, nyomáson és térfogaton egyenlő számú molekulát tartalmaznak.1827-ben Brown botanikus megfigyelte a virágporszemcsék mozgását mikroszkóp alatt. A jelenség magyarázata szintén a molekulák létére vezethető vissza.
A XIX. század hatvanas éveiben kialakuló kinetikus gázelmélet már tudatosan használta az atom és a molekula fogalmát. A gázokban lévő részecskék mozgására vezette vissza a gáz hőmérsékletét és nyomását.
- Az elektron felfedezése
Az atom fogalma a kémia fejlődésének köszönhetően vált elfogadottá. Ugyancsak a kémiai kísérletek tapasztalatai vezettek el oda, hogy az atom nem egy oszthatatlan részecske, hanem töltéssel rendelkező elemi részeket tartalmaz.
Ezen elemi részek közül először az elektront fedezték fel. De mivel az atom elektromosan semleges, ebből következik, hogy az atomban pozitív töltésű részecskének is kell lenni.Az elektron létét bizonyítják a következő kísérletek, jelenségek:
1) Elektrolízis
2) Millikan-kísérlet
3) Hidegemisszió
4) Richardson-hatás
5) Izzóelektromos hatás
6) Katódsugárzás- Elektrolízis
Elektrolitoknak nevezzük az ionokat tartalmazó folyadékokat.
Helyezzünk elektrolitba két elektródát és kapcsoljunk rá áramforrást.
A körben mérhető áramerősség és az idő ismeretében megkapjuk az elszállított töltés nagyságát. Az áram az ionok vándorlásának következménye: az ellentétes előjelű töltéssel rendelkező ionok különböző elektródákhoz vándorolnak, semlegesítődnek, s ott általában gáz vagy szilárd alakban kiválnak.
A katódon elektron felvétel, az anódon elektron leadás történik.
A kinyert anyagok mennyisége, és így az ionok darabszáma kémiai mérésekkel határozható meg.Az elektrolízisre vonatkozó törvényeket Faraday fogalmazta meg:
Elektrolízis során, az elektródán kivált anyag tömege egyenesen arányos az elektrolizáló áram erősségének és az elektrolízis idejének a szorzatával, az arányossági tényező az elektrokémiai egyenérték (k).
Az elektrokémiai egyenérték számértéke kifejezi, hogy 1C töltés hatására az adott anyagból mennyi válik ki elektrolízis során.

Egy molnyi anyag kiválasztásához annyiszor 96 500 C töltés szükséges, amennyi az illető anyag vegyértéke.
- Millikan-kísérlet
Millikan (1868-1953) angol fizikus vízszintesen elhelyezett kondenzátorlemezek közé olajcseppeket porlasztott, majd ezeket mikroszkópon keresztül figyelte meg. Egy olajcseppet kiválasztva addig változtatta az elektromos mezőt, míg a porlasztás során töltést kapott olajcsepp lebegni kezdett.

Az egyensúlyt a gravitációs erő és az elektrosztatikus erő egyenlősége okozta. Az olajcsepp mérete optikai úton meghatározható, így a következő egyenlőség írható fel:

ahol m az olajcsepp tömege, V a térfogata, ρ a sűrűsége, Q a töltése, E a kondenzátor lemezei közötti térerősség, U a feszültség, d a távolság. Az U feszültség és a lemezek d távolsága mérhetők, így megkaphatjuk az olajcsepp töltését.
Millikan azt tapasztalta, hogy minden esetben az eleminek nevezhető töltés egész számú többszörösét kapta, vagyis az elemi töltés a legkisebb töltésegység:
- Hidegemisszió
Vigyünk fémtárgyra töltést, amely — amint az elektrosztatikából tudjuk — az azonos töltések taszítása következtében a fém felületén helyezkedik el. Nagyon nagy töltés esetében akkora lehet a taszítás, hogy a töltés egy részét kinyomja a felületből, különösen a csúcsok közelében. A környező gázmolekulák zavaró hatását kiküszöbölhetjük, ha a fémtárgyat légritkított térbe helyezzük. A jelenség neve hidegemisszió és arra utal, hogy a töltés valamilyen töltéshordozóhoz tartozik.

- Richardson-hatás

Richardson (1879-1959) angol fizikus figyelte meg azt a jelenséget, hogy a fémekből minden külső hatás nélkül is kilépnek a negatív töltések.
Légritkított edénybe egymással szemben két elektródát helyezünk el, az egyiket leföldeljük, a másikra gyenge pozitív feszültséget adunk. Azt tapasztaljuk, hogy az elektródák között áram indul meg.
A jelenség magyarázata a következő: a töltés valamely töltéshordozóhoz kapcsolódik, amely a hőmozgás következtében kiléphet a felületből. A földelt elektródából spontán kilépő negatív töltéshordozó nem esik vissza az elektródára, hanem engedve a gyenge vonzó hatásnak, a másik elektródára kerül.
- Izzóelektromos hatás
Magas hőmérsékleten erősen megnő a Richardson-hatás, az izzó fémből már tömegesen távozik a negatív töltés. Ez az izzóelektromos jelenség vagy termikus emisszió.
- Katódsugárzás
Helyezzünk erősen légritkított térbe két elektródát, s kapcsoljunk rájuk áramforrást! Nagyon kis gáznyomás esetén a katód egy láthatatlan sugárzást bocsát ki, amely abból vehető észre, hogy a katóddal szemben, ahol a sugárzás az üvegburát éri, fényjelenség jön létre, amennyiben az üveg belső felületét fluoreszcens anyaggal vonták be. Ez a sugárzás a katódsugárzás.

A katódsugárzást J. J. Thomson (1856-1940) vizsgálta először. 1897-ben végzett kísérleteiben elektromos és mágneses terek segítségével a katódsugárzásban megjelenő részecske eltérülését vizsgálta, s ennek segítségével meghatározta annak fajlagos töltését. Az elemi töltés ismeretében kiszámítható volt a részecske tömege is, ezért ezt az időpontot tekintjük az elektron felfedezésének.
Thomson által elvégzett mérés egyszerűsített változata a következő:

A katódsugárcsőben izzókatódot alkalmazunk, a katód és az anód közé ismert gyorsítófeszültséget kapcsolunk. Az anód nyílásán keskeny nyalábban áthaladó, közel azonos sebességű elektronok ismert erősségű homogén mágneses térben ugyanazon a körpályán mozognak, amelynek sugara meghatározható.
A levezetés a következő:
A körmozgásra vonatkozóan a centripetális erőt a mágneses Lorentz-erő szolgáltatja:

innen 
ahol m az elektron tömege, v a sebessége, q a töltése, R a körpálya sugara, B a mágneses indukció.
A gyorsítási munka megadja az elektron mozgási energiáját (feltéve, hogy a gyorsítási feszültség néhány százezer V alatt marad, s így az elektron sebessége nem közelíti meg a fénysebességet):

Helyettesítsük ebbe a sebesség kifejezését:

Így a fajlagos töltésre adódik:

Az elemi töltés ismeretében az elektron tömege:
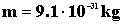
Ezzel tehát az elektron polgárjogot nyert, mint az "oszthatatlannak" hitt atom egyik alkotórésze.
- Elektrolízis
- A kvantumfizika születése
A kvantumfizika a fizikának az a része, amely az elektron atomon belüli viselkedését írja le.
Sok kísérlet, kísérleten alapuló elmélet vezetett el odáig, hogy a tudósok létrehozzanak egy olyan modellt, amely segítségével az elektronok atombeli állapota jellemezető. Ezek közül a legfontosabbak:- a hőmérsékleti sugárzás intenzitás-hullámhossz grafikonjának matematikai leírása,
- a fényelektromos hatás magyarázata,
- színképelemzés,
- atompálya energiaszintjének meghatározása, amelyet Franck és Hertz végzett el,
- az elektron hullámtermészetének felismerése.
Nézzük ezeket részletesebben!
- Hőmérsékleti sugárzás
Tapasztalati tény, hogy a testek minden hőmérsékleten hőt sugároznak ki elektromágneses hullámok formájában. Ez a hőmérsékleti sugárzás.
Az elektromágneses sugárzás intenzitása természetesen nő a hőmérséklet növekedésével, emellett a sugárzás hullámhossz-eloszlása is változik a hőmérséklettel.
A XIX. század végére a hősugarakkal kapcsolatban már nagyon sok megállapítás gyűlt össze. Ezek közül néhány:- Stefan-Boltzmann megállapították, hogy egységnyi felületrő1 egységnyi idő alatt kisugárzott energia arányos a test abszolút hőmérsékletének negyedik hatványával.

- Megfogalmazták, hogy abszolút fekete test az az idealizált test, amely minden érkező sugárzást teljes egészében elnyel. (Jó közelítéssel ilyen lehet egy kicsiny nyílású üreg).
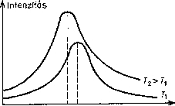 A Wien-féle eltolódási törvény szerint minden hőmérséklethez tartozik egy hullámhossz, ahol a sugárzás intenzitása maximális. Ez a hullámhossz fordítva arányos a hőmérséklettel.
A Wien-féle eltolódási törvény szerint minden hőmérséklethez tartozik egy hullámhossz, ahol a sugárzás intenzitása maximális. Ez a hullámhossz fordítva arányos a hőmérséklettel.
A kísérleti tapasztalatok alapján megállapította, hogy az abszolút hőmérséklet és a hullámhosszmaximum szorzata állandó.

Az intenzitás-hullámhossz grafikont több fizikus is megpróbálta matematikailag leírni, de ez a klasszikus fizika keretein belül nem sikerült.
Max Planck (1858-1947) vizsgálatait szintén az a cél vezérelte, hogy magyarázatot találjon az előbbi törvényekre. 1900-ban kutatásai során arra a meglepő eredményre jutott, hogy akkor kap kielégítő magyarázatot a tapasztalati eredményekre, ha feltételezi a következőket:
Egy test részecskéi (atomok, molekulák vagy ionok) nem folytonosan, hanem elkülönült adagokban (kvantumokban) sugároznak ki és nyelnek el energiát. Ez a véges energiaadag arányos a sugárzás frekvenciájával:
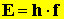
Az arányossági tényező
 , amelyet ma Planck-állandó néven emlegetünk.
, amelyet ma Planck-állandó néven emlegetünk. Így jelenik meg először az energiaadag, energiakvantum fogalma. Ez a korabeli fizikusok számára megdöbbentő ellentmondásban volt a klasszikus szemlélettel, ami a folytonos energiaközlés lehetőségét természetesnek tartja.
Planck elmélete nemcsak a hőmérsékleti sugárzás hullámhossz szerinti eloszlását írta le sikeresen, hanem tartalmazta a Wien-féle eltolódási törvényt és a Stefan-Boltzmann-törvényt is. Ilyen sikeres elméletről azt gondolhatnánk, hogy azonnal ismertté és elfogadottá vált a fizikusok körében.
Nem így történt. Hosszú évekig tartott, amíg felismerték Planck munkásságának jelentőségét, amit az is mutat, hogy csak 1918-ban kapott Nobel-díjat az energiakvantum felfedezéséért.Önéletrajzában fanyar humorral így ír erről: „Valamely új tudományos igazság nem úgy szokott győzelemre jutni, hogy az ellenfelek meggyőzetnek, és kijelentik, hogy megtértek, hanem inkább úgy, hogy az ellenfelek lassanként kihalnak, és a felnövekvő nemzedék már eleve hozzászokik az igazsághoz…”
- Stefan-Boltzmann megállapították, hogy egységnyi felületrő1 egységnyi idő alatt kisugárzott energia arányos a test abszolút hőmérsékletének negyedik hatványával.
- Fényelektromos hatás
Ismert az a jelenség, hogy fény hatására a fémek felületéről elektronok léphetnek ki. Ez a fotoeffektus, azaz a fényelektromos jelenség.
A mérések azt bizonyítják, hogy csak a fény frekvenciájától függ, hogy egy fém felületéről kilép-e az elektron, de a fény intenzitásától nem.
A vörös fény általában nem, az ibolya ritkán, az ultraibolya sok fém esetén elegendő a jelenség bekövetkezéséhez.
A fény intenzitása csak a kilépő elektronok számát határozza meg, a kilépés bekövetkezését és a kilépő elektron energiáját nem.
A klasszikus szemlélet alapján ezt a tényt nem lehetett magyarázni.
A problémát Einstein oldotta meg. Érdekesség, hogy Einstein a fotoeffektusra adott magyarázatáért, és nem a relativitáselmélet megalkotásáért kapta a Nobel-díjat.
Abból indult ki, hogy a fény nemcsak hullámtermészettel, hanem részecske- természettel is rendelkezik. A fény részecskéit fotonoknak nevezte.
- A fény nem folytonosan, hanem adagokban, kvantumokban szállítja az energiát. A fénykvantum a foton. Amikor a foton ütközik az atom elektronjával, akkor átadja annak energiáját.
- Egy energiakvantum által szállított energia nagysága arányos a fény frekvenciájával.
- Az anyagban kötött elektron egyszerre mindig csak egy fotonnal találkozik, amelynek energiája nagyobb kell, hogy legyen az elektron kötési energiájánál ahhoz, hogy az elektron kiszabaduljon.
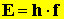
A foton energiájának egy része tehát a kilépési munkát szolgáltatja, másik része pedig az eltávozó elektron mozgási energiáját adja.
A következő összefüggés írható fel:
A fényelektromos jelenség gyakorlati alkalmazását látjuk a fotocellák működésekor.

- Egy üvegből készült kisülési csövet úgy alakítanak ki, hogy a katód felülete könnyen megvilágítható legyen.
- A katód felületét olyan fémmel vonják be, amelyben az atomok legkülső elektronjainak energiaszintje közel helyezkedik el a nulla szinthez. Erre legalkalmasabbak az alkálifémek, amelyek a periodikus rendszer I. A oszlopában helyezkednek el.
- Ha a katódot nem világítjuk meg, akkor az áramkör nyitott. A kisülési csőben a két elektróda között szakadás van.
- Ha a katódot megvilágítjuk, akkor abból elektronok lépnek ki, zárul az áramkör. Ilyenkor az áramerősség-mérő áramot jelez.
Az elektron kilépési munkájának kísérleti meghatározása

- Egy fotocellát ellentétes polaritással kapcsolunk be az áramkörbe.
- Változtassuk úgy a feszültség nagyságát, hogy a kezdeti elektronáramlás az ellentér hatására éppen megszűnjön.
- Az így mérhető feszültséget megszorozva az elektron töltésével, megkapjuk azt a munkát, amit a tér végzett, miközben a fémlapból valamilyen sebességgel kilépő elektront lelassította. Ez tehát éppen egyenlő az elektron kezdeti mozgási energiájával.

Kísérlet a fényelektromos hatás kimutatására
Fotocella nélkül is kimutatható a fényelektromos hatás.
Helyezzünk el szigetelő tartóállványon egy cinklemezt, melyet előzőleg dörzspapírral csiszoljunk meg. A lemezt kössük össze egy elektroszkóppal, majd töltsük fel negatív töltéssel.
Ha a teremben nem különösebben párás a levegő, akkor az elektroszkóp azt jelzi, hogy alig csökken a töltés a lemezen. Ha viszont a lemezt ultraibolya fénnyel világítjuk meg (ehhez használhatunk kvarclámpát is), akkor rohamos töltéscsökkenést észlelünk.
A cink ugyanis alkáliföldfém, látható fényben nem lépnek ki belőle elektronok, ultraibolya fényben megindul a fotoeffektus, az elektronok kilépése, melyeket a cinklemez maradék negatív töltése messze taszít a lemeztől. - Vonalas színkép és energiaszintek
A XIX. század elején látták először a vonalas színképet. A színképek kísérleti tanulmányozása az egész századon át folytatódott, egyre inkább tökéletesedett.
Ezt a tevékenységet spektroszkópiának nevezzük.A század spektroszkópiával foglalkozó szakemberei nem is sejtették, hogy tevékenységükkel az atomfizika legfontosabb technikáját teremtik meg, mivel az általuk megmért színképvonalak hullámhosszaiból az atomi elektronok energiáit lehetett meghatározni.
A spektroszkópiát fokozatosan kiterjesztették a látható tartományon kívül az infravörös és az ultraibolya tartományra is. Minden tartományban azt észlelték, hogy
- az izzó gázok színképe vonalas,

a Na vonalas színképe - az izzó szilárd testek és folyadékok színképe folytonos.

A kibocsátási vagy emissziós színkép
A magas hőmérsékleten izzó szilárd és folyékony testekből kibocsátott fényben a fehér fény összes színárnyalata megtalálható. Színképük folytonos. A folytonos színkép független a fényt kibocsátó test anyagi minőségétől.

A folyadékok és szilárd anyagok atomjainak külső elektronjai egymáshoz közel vannak, a kvantumfizika törvényei szerint nem tudnak egymástól függetlenül viselkedni, esetükben nem jön létre vonalas színkép.
Az izzó gőzök által kibocsátott fény is felbontható, de színképük nem folytonos, hanem jellegzetes, színes, meghatározott hullámhosszúságú vonalakból áll. Az izzó gázok és gőzök fénye vonalas színképet hoz létre. A vonalas színkép a gőz, gáz anyagi minőségére jellemző.

Az izzó gázok atomjai nagy távolságra vannak egymástól, az atomi elektronok egymástól függetlenül, egyformán viselkednek, egymással megegyező energiaszintjeik vannak. Ez eredményezi színképükben az éles vonalakat.

A nátrium vonalas színképeAz elnyelési vagy abszorbciós színkép
Amikor az izzó gőzön (vagy gázon) fehér fényt bocsátunk keresztül, az izzó gőzök elnyelik a fehér fényből azokat a színeket, amelyeket egyébként maguk is kibocsátani képesek. Ilyenkor az emissziós színkép színes vonalainak helyén az ernyőn fekete (elnyelési) vonalakat látunk.

Az elnyelési színkép ugyanúgy jellemző az anyagi minőségre, mint az emissziós színkép.
Elnyelési színkép esetén a gázban lévő atomok elektronjai a fehér fényben lévő fotonok elnyelésével kerülnek magasabb energiájú, gerjesztett állapotba, majd nagyon rövid idővel ezután vissza is jutnak alacsonyabb energiákra. Tehát az elnyelt fotonokat ki is sugározzák. A kisugárzás azonban véletlenszerű, a tér minden irányában történhet, tehát csekély a valószínűsége, hogy a keletkező fotonok az eredeti megvilágítás irányában haladnak tovább. Ezért jöhetnek létre hiányzó, sötét vonalak az elnyelési képben.

A legerősebb elnyelési vonalak a Nap színképébenA spektroszkóp
A színképvonalak jellemzőek a fényt kibocsátó vagy elnyelő gázhalmazállapotú test anyagi minőségére. Ezért a vonalas színképek vizsgálata, a színképelemzés, az anyagvizsgálatok egyik fontos és érzékeny módszere.
A színképelemzéshez hullámhossz-skálával ellátott spektroszkópot használnak. A spektroszkóp egyik legegyszerűbb fajtájának elrendezését az ábra mutatja.
 A spektroszkóp egyik csöve (S) az L lámpával megvilágított skálát vetíti a prizmára, amely onnan visszaverődve a vizsgáló távcsőbe (T) jut.
A spektroszkóp egyik csöve (S) az L lámpával megvilágított skálát vetíti a prizmára, amely onnan visszaverődve a vizsgáló távcsőbe (T) jut.
A másik cső (K) elé, rendszerint üvegcsőben (és elektromos árammal gerjesztve), a vizsgált izzó gőzt helyezik. Ennek fényét a prizma színeire bontva, ugyancsak a vizsgáló távcsőbe juttatja. A színképvonalak számából és a skálán leolvasott helyéből (hullámhosszából) a gőz anyagi minősége, összetétele meghatározható. - az izzó gázok színképe vonalas,
- Franck-Hertz-kísérlet
1914-ben James Franck (1882-1964) és Gustav Hertz (1887-1975) döntő és közvetlen kísérleti bizonyítékot talált az atomi energiaszintek létezésére.
Miközben elektronok mozgását tanulmányozták higanygőzben külső elektromos mező hatására, észrevették, hogy amennyiben az elektronok mozgási energiája 4,9 eV-nál nagyobb, a higanygőz 254 nm hullámhosszúságú ultraibolya fényt sugároz ki.
Feltételezték, hogy a higanyatomnak van egy olyan energiaszintje, amely 4,9 eV-tal magasabban van az alapállapotnál, (a legalacsonyabb energiájú állapotnál). Az atom úgy kerül erre az energiaszintre, hogy egy elektronnal ütközik, az elektron mozgási energiája lecsökken az atom belső energiája megnő.
Nagyon kis idővel a gerjesztés után a higanyatom elektronja újra alapállapotba kerül, miközben egy fotont (egy energiaadagot) sugároz ki. A 254 nm hullámhosszúságú foton energiáját a Planck-formula alapján számíthatjuk ki, melyben a frekvenciát a λ hullámhosszból a c fénysebesség segítségével fejezhetjük ki :

amely pontosan megegyezik a felgyorsított elektron kísérletileg meghatározott mozgási energiájával.
A Franck-Hertz-kísérlet tehát közvetlen bizonytékát adja a higanyatom 4,9-eV-os energiaszintjének létezésének.
Munkájáért Franck és Hertz 1925-ben Nobel-díjat kapott. - Röntgensugarak
Az első fizikai Nobel-díjat 1900-ban Wilhelm Röntgen (1845-1921) kapta a róla elnevezett sugárzás felfedezéséért. A felfedezés 1895-ben, véletlenül történt, amikor Röntgen nagyfeszültségű kisülési csövekkel kísérletezett. Nem tudta megfejteni, milyen sugárzást fedezett fel (X-sugárzásnak, vagyis ismeretlennek nevezte el, ami az angol nyelvben a mai napig megmaradt - X rays), de számos tulajdonságát, legfőképpen rendkívüli áthatoló képességét a felfedezés után néhány héten belül megállapította.
A felfedezést követő hatodik héten már megtörténtek az első orvosdiagnosztikai alkalmazások is, a fizikai felfedezések közül ennél gyorsabb gyakorlati alkalmazásra valószínűleg soha nem került még sor. Azóta nemcsak az orvostudományokban, hanem rendkívül sok más területen is széles körben alkalmazzák a röntgensugarakat. Sajnálatos, hogy az alkalmazások első néhány évtizedében még nem ismerték fel a röntgensugaraknak az emberi szervezetre gyakorolt káros hatását, hosszú ideje azonban már minimálisra csökkentették az egészségkárosítás kockázatát.
A röntgensugarak keletkezését és tulajdonságait csak a Planck-Einstein-féle fotonképpel és a Bohr által bevezetett atomi energiaszintekkel lehetett megmagyarázni, ezzel újabb példát mutathatunk be az elektromágneses sugárzás kvantumos természetére. A röntgensugarak keletkezését a fényelektromos hatás megfordításának is tekinthetjük.
- A fényelektromos jelenség úgy jön létre, hogy egy fém felületét fénnyel megvilágítjuk, ennek hatására elektronok szabadulnak ki a fém felületéből.
- A röntgensugarakat viszont úgy keltik, hogy fémfelületeket elektronokkal bombáznak, ennek következtében a fémből elektromágneses sugarak, röntgensugarak lépnek ki.
A röntgensugarakról teljes biztonsággal csak az 1910-es években mutatták ki, hogy nagyfrekvenciájú elektromágneses hullámok, vagyis nagyenergiájú fotonok.

Az ábrán egy régi típusú és egy mai röntgencsövet láthatunk, mindkettő
belsejében vákuum van. A mai eszközökben az elektronok izzókatódból lépnek ki, majd az általában néhányszor tízezer voltos pozitív feszültségre kötött anódba
csapódnak.Megjegyzés: A korszerű röntgencsövekben az elektronok becsapódása olyan heves, hogy az üreges szerkezetű anódot erős vízsugárral hűteni kell, máskülönben nagyon rövid idő alatt szétolvadna.
Az anódba csapódó elektronok különböző hullámhosszúságú röntgensugarakat keltenek.

Az ábrán egy tipikus hullámhossz szerinti intenzitás-eloszlást láthatunk. Az intenzitásgörbén megfigyelhetünk:
- A folytonos röntgensugárzást fékezési sugárzásnak is hívjuk, mert ez az anódba csapódó elektronok lefékeződése miatt keletkezik. A lefékeződő elektronok nagy negatív gyorsulással állnak meg, és a gyorsuló töltések elektromágneses hullámokat sugároznak ki: ezek a folytonos tartomány röntgenfotonjai.
- Az intenzitás-csúcsok akkor keletkeznek, amikor az anód anyagába becsapódó elektronok olyan nagy mozgási energiával rendelkeznek, hogy képesek a legerősebben kötött, az atommaghoz legközelebbi, legbelső pályákon lévő elektronokat is kilökni. Ezek az úgynevezett 1s pályán lévő elektronok, melyeket régebbi szóhasználat szerint a K héjon lévő elektronoknak hívunk.
Ha az anódba csapódó elektron kilök egy K elektront, tehát a K héjon egy betöltetlen, mélyen fekvő energiaszint marad, akkor kevesebb, mint egy nanoszekundumon belül egy magasabb energiaszinten lévő elektron ugrik erre a szintre (az energiaminimumra törekvés elve szerint). Legvalószínűbb, hogy eggyel vagy kettővel magasabban lévő héjról, tehát az L vagy az M héjról ugrik elektron a K héj betöltetlen állapotába. Ezzel az elektron alacsonyabb energiájú állapotba kerül, ami a két energiaszint közötti energiakülönbségnek megfelelő foton kisugárzásával jár. A mélyen kötött állapotokban ez az energiakülönbség olyan nagy, hogy nagy energiájú röntgen-foton keletkezik a folyamatban.
- Az elektron hullámtermészete
Az atomok szerkezetének megismerése szempontjából egy fontos lépcső volt Louis de Broglie 1924-ben tett feltevése. Abból a szimmetriából indult ki, hogy a korábban hullámnak hitt fénynek is van részecsketermészete, akkor a részecskéknek is kell, hogy legyen hullámtermészete. Tehát az elektronok vagy a protonok bizonyos helyzetekben hullámként is viselkedhetnek.
Ha az elektron lehet hullám is, akkor kell, hogy legyen frekvenciája és hullámhossza.
De Broglie úgy gondolta, hogy a szabadon mozgó elektronok hullámhosszát és frekvenciáját a fotonéhoz hasonló összefüggések határozzák meg.Foton energiájának, tömegének és impulzusának meghatározása
Atomfizikában az impulzus szokásos jele: pA foton energiája:

A foton mozgási tömege:

A foton lendülete:

De Broglie érvelése szerint ugyanezeknek az összefüggéseknek érvényesnek kell lenni az elektronokra is.
Tehát, ha egy m tömegű elektron v sebességgel mozog és p a lendülete, akkor:Az elektron lendülete:

Az elektron hullámhossza (de Broglie hossz):

Az elektron frekvenciája:

De Broglie elméleti feltevését három év múlva két amerikai kutató Devisson és Germer igazolták kísérlettel. Alumínium kristályon röntgensugár és elektronnyaláb elhajlási képét vizsgálták. A két elhajlási kép hasonló volt abban az esetben, amikor az elektronhullám hullámhossza közel azonos volt a röntgensugár hullámhosszával.

- Elektronmikroszkóp
Egy mikroszkóp felbontóképessége, azaz nagyításának határa attól függ, hogy mekkora a leképezésre használt hullám hullámhossza.
Látható fénnyel működő mikroszkóp felbontóképessége néhány száz nanométer (kb. 10-5 m). Ez néhány ezer atom együttes átmérőjének felel meg.
Röntgensugárzással sokkal nagyobb felbontóképességet lehetne elérni. De itt az a probléma merül fel, hogy nem található olyan anyag, amelyből olyan lencsét lehetne készíteni, hogy a röntgensugárzást fókuszálni lehessen.
Amikor bizonyítottá vált, hogy az elektron rendelkezik hullámtulajdonsággal, és hullámhossza összemérhető a röntgensugárzás hullámhosszával, kézenfekvő volt, hogy elektronnyalábbal működő mikroszkópot készítsenek.
Az első elektronmikroszkóp 1931-ben készült el. Az elektronok egy izzó katódból lépnek ki, és 10 kV - 100 kV gyorsító feszültséggel gyorsítják azokat. Az elektronnyalábot mágneses és elektromos lencsék segítségével fókuszálják.
- Atommodellek
- Thomson-modell (puding-modell)
A XX. század elejére világossá vált, hogy az atomban található elektronok ugyanazok, mint a katódsugárzás részecskéi.
Magyarázatra várt azonban
- mi tartja össze az atomot,
- milyen szerkezetű,
- hogyan magyarázható a kívülről tapasztalt semlegesség.
J. J. Thomson talált először érveket amellett, hogy az atomban található elektronok száma nem túl nagy, az atom tömegének nagy részét a pozitív töltésű rész adja.
Elképzelése szerint az atom egész térfogatát kitölti a folytonosan elosztott pozitív rész, s ebben vannak beágyazva az igen kis méretű elektronok. Ezek vagy nyugalomban vannak az atom középpontjában, vagy meghatározott sugarú pályákon körben keringenek.A modell — bár nem sokáig volt elfogadható — igen pozitív szerepet játszott a kutatásokban, mivel
- teljes egészében figyelembe vette a klasszikus elektrodinamika törvényeit (pl. hogy a gyorsuló töltés sugároz),
- és itt vetődött fel először az elektronburok héjszerkezete.
A modell azért nem maradt sokáig érvényben, mert hamar kiderült, hogy az atomban viszonylag sok hely van, és így nem lehet folytonos kitöltésű.

- Rutherford-modell (Naprendszer-modell)

Rutherford (1871-1937) munkatársaival kísérleteket végzett az atom szerkezetének vizsgálatára. Nagy energiájú héliumatommagok vékony fémfólián való áthaladásának vizsgálata során a tapasztalat szerint a pozitív töltésű héliumatommagok nagy számban áthaladtak a vékony anyagrétegen.
Ez azt mutatja, hogy- az atom igen "szellős" szerkezetű, tömegének nagy része igen kis helyre koncentrálódik,
- néhány részecske jelentősen, nagy szögben elkanyarodott, szóródott, ami csak nagy pozitív töltésű centrumokkal való ütközéssel magyarázható.
Ez volt a híres szórási kísérlet.

A konkrét kísérleti eredmények értelmezésével született 1911-ben meg az újabb atommodell. Eszerint
- az atom középpontja az atom méreténél három nagyságrenddel kisebb pozitív mag,
- a mag körül, mint bolygók a Nap körül, keringenek az elektronok,
- az elektronokat az elektrosztatikus vonzóerő tartja körpályán.
A körpályán keringő elektron azonban, mivel gyorsul, ezért sugároz, és így fokozatosan elveszti energiáját, az atom tehát nem lehetne stabil. A modell ezen hibája hamar nyilvánvalóvá vált.

- Bohr-modell
Niels Bohr (1885-1962), Rutherford tanítványa a hidrogénatomra vonatkozóan új modellt alkotott. Hogy mestere, Rutherford modelljének hiányosságait megoldja, önkényes feltevéseket vezetett be. Ezek a Bohr féle kvantumfeltételek.
- Az atom elektronjai csak meghatározott pályákon keringhetnek a mag körül.
- Az ilyen pályán keringő elektron - a klasszikus fizika törvényeivel ellentétben - nem sugároz.
- Az atom csak akkor sugároz, ha az elektron az egyik pályáról a másikra ugrik. Ilyenkor a két pálya közötti energiakülönbséget az elektron egyetlen foton formájában kisugározza, amelynek így az energiája:

A modellből levezethető:
- A hidrogénatomban lévő elektron körpályáinak sugara:

- Az n-dik pályán keringő elektron teljes energiája:

A modell előnye:
- Hidrogénatom és egy elektront tartalmazó ionok esetén a számított és a mért színképvonalak megegyeztek. Ez bizonyítja az atomok energia felvételének kvantumosságát.
- magyarázatot adott a diszkrét energiaszint létezésére.
A modell hátránya:
- Több elektronos atomok esetén nem adott jó értéket.
- A modell alapján a kémiai kötéseket nem lehetett értelmezni.
A modellt később Sommerfeld (1868-1951) fejlesztette tovább, kiegészítve a körpályákat ellipszispályákkal.
A Bohr-modellt a kvantumszámok bevezetésével fejlesztették tovább.
- Kvantumszámok
A kötött elektron 4 kvantumszámmal jellemezhető:
- Főkvantumszám
Az atommag és az elektronfelhő átlagos távolságára ad felvilágosítást.
Jele: n
Értéke: 1, 2, 3…(pozitív egész számok) - Mellék-kvantumszám
Az elektronfelhő alakjára ad felvilágosítást.
Jele: l
Értékei: 0, 1, 2…(n-1)l
állapot
0
s
1
p
2
d
3
f
4
g
- Mágneses-kvantumszám
Az azonos alakú, tehát azonos mellék-kvantumszámú pályák irányára ad felvilágosítást.
Jele: m
Értékei: -l, (-l+1)…..0…..+l
Pl.:
n l m Atompályák száma 3 0 0 9 1 -1, 0, +1 2 -2, -1, 0, 1, 2 - Spinkvantumszám
Az elektronfelhő impulzusmomentumára, és ebből adódóan mágneses tulajdonságára ad felvilágosítást.
Jele: ms
Értéke: +1/2 vagy –1/2
- Főkvantumszám
- Atompályák energia sorrendje
Az atompályák energiája attól függ, hogy az adott atompálya
- milyen távol helyezkedik el az atommagtól,
- milyen az alakja.
Ez alapján az atompályák energia szerinti sorrendje az atommagtól távolodva:
E1s<E2s< E2p< E3s <E3p<E4s< E3d< E4p< E5s< E4d< E5p< E6s< E4f< E5d< E6p< E7s
- Kvantummechanikai atommodell
1925-27 között Schrödinger (osztrák) és Heisenberg (német) fizikusok a mikrorészecskék mozgását leíró mechanikát dolgoztak ki.
- Schrödinger a mikrorészecskék viselkedésének fizikai leírásánál azok hullámtulajdonságát használta ki.
- Heisenberg a mikrorészecskék viselkedésének fizikai leírásánál a kvantumosságot helyezte előtérbe.
A későbbiek során kiderült, hogy a két elmélet megfelel egymásnak, beigazolva az anyag kettős természetét.
Heisenberg leírásában szerepel a mikrorészecskékre vonatkozó határozatlansági reláció. E szerint:
Egy részecske helyét és impulzusát egyidejűleg nem lehet tetszőleges pontossággal megadni. Elméletileg levezethető, hogy a két mennyiség bizonytalanságának szorzata legjobb esetben is a Planck-állandó nagyságrendjébe esik.

Ezt az összefüggést nevezzük a Heisenberg-féle határozatlansági relációnak.
A kvantummechanikai atommodell szerint

- Az elektron nem pontszerű részecske, amely az atommag körül kering.
- A modell az elektront állóhullámokkal jellemzi, amelyet az atommag elektromos tere tart fogva.
- Az atomba zárt elektron csak meghatározott alakú és térbeli kiterjedésű állóhullámot alkothat.
- Minden hullámalakhoz meghatározott energiaérték tartozik.
- Az atomok által kibocsátott vagy elnyelt fotonok energiája az állóhullámokhoz tartozó energiaértékek különbségével egyenlő.

A modellt a Pauli-elv és a Hund-szabály tette teljessé.
- Thomson-modell (puding-modell)
- Történeti áttekintés
- Célként jelölte meg, az anyag belső szerkezetének megismerését.
- Gázokra vonatkozó törvényekkel foglakozott.
- Többszörös súlyviszonyok törvénye
- Atomsúly-táblázat készítése
- Katódsugárzás vizsgálata
- Az elektron fajlagos töltésének meghatározása
- Atommodell
ATOMFOGALOM KIALAKULÁSA |
||
| Kb.Kr. e. 400 | Démokritosz | Spekulatív úton eljutott az atom fogalmához |
| XVII. sz. | Boyle | |
| XVIII. sz. | Lavoisier | Definiálta az elem fogalmát |
| XIX. sz. | Proust | Állandó súlyviszonyok törvénye |
| Dalton | ||
| Gay-Lussac | Gáztörvény | |
| Avogadro | Gáztörvény | |
ELEKTRONFOGALOM KIALAKULÁSA |
||
| XIX. sz. | Faraday | Elektrolízisre vonatkozó törvények |
| XX. sz. | Milliken (1909) | Elemi töltés meghatározása |
| Richardson | Fémekből elektronok épnek ki | |
| Edison hatás | Izzó fémekből az elektronkilépés intenzívebb | |
| Thomson | ||
| Planck (1900) | Kvantáltság fogalma | |
| Einstein (1905) | Fotoeffektus | |
| Röntgen (1901) | Röntgensugarak | |
| Franck-Hertz (1914) | Atomi energiaszintek létezésének bizonyítása | |
| De Broglie (1924) | Elektron kettős természete | |
| Devisson és Germer (1927) | Az elektron hullámtermészetének kísérleti bizonyítása | |
ATOMMODELLEK |
||
| Rutherford (1911) | Naprendszer-modell | |
| Bohr (1913) | Bohr-modell | |
| Schrödinger és Heinsenberg (1925-27) | Kvantummechanikai atommodell | |