1. Gravitációs mező

    Az anyagnak két megjelenési formája van:

    1. a korpuszkuláris anyag, és
    2. a mező.

    A korpuszkuláris anyag a részecskékből álló anyag. Ilyen a gáz, folyékony és szilárd halmazállapotú anyag, de ide tartozik a proton, neutron stb. is. 

    A mező az anyag egyik sajátos formája, amely rendelkezik pl. energiával.

    Az elektromosan töltött testeket az elektromos mező, a mágneseket a mágneses mező veszi körül, a tömeggel rendelkező testeket pedig a gravitációs mező.

    Két tömeggel rendelkező test úgy lép kölcsönhatásba egymással, hogy az egyik tömeg által létrehozott gravitációs mező hat a mezőbe helyezett másik tömeggel rendelkező testre.

    A gravitációs kölcsönhatás jellemzése

    • A gravitációs kölcsönhatás mindig csak vonzásban nyilvánul meg.
    • Az anyag kölcsönhatásai közül a gravitációs kölcsönhatás a leggyengébb.
    • A gravitációs mező hatása nem árnyékolható le.
    • A gravitációs mező egyetemes. Ez azt jelenti, hogy a világmindenség minden részecskéjéhez tartozik egy gravitációs mező. Így a világmindenség minden részecskéje kölcsönhatásban van minden részecskével.
  2. Gravitációs mező jellemző tulajdonságai
    1. A gravitációs mező forrásos mező.
      A gravitációs mező forrásai a tömeggel rendelkező testek. Ahol tömeg van, ott kialakul a gravitációs mező.
    2. A gravitációs mező konzervatív mező.
      Ez azt jelenti, hogy a gravitációs mezőben fellépő gravitációs erő által két pont között végzett munka nagysága nem függ az útpálya hosszától, csak a két pont helyzetétől.
    3. A gravitációs mező örvénymentes mező.
      Ez azt jelenti, hogy a mezőben fellépő konzervatív gravitációs erő által zárt görbe mentén végzett munka összege nulla.
  3. Newton-féle gravitációs törvény

    Tömeggel rendelkező testek között fellépő kölcsönhatást Newton fogalmazta meg 1686-ban.

    Bármely két tömeggel rendelkező test között fellép a gravitációs erő.
    Ez az erő egyenesen arányos a két test tömegének szorzatával, és fordítottan arányos a két test közötti távolság négyzetével. Az arányossági tényező a rgavitációs-állandó.

    A gravitációs-állandót Newton felismerését követően majdnem 100 évvel később Cavendish állapította meg.

  4. A gravitációs állandó meghatározása
    Cavendish-kísérlet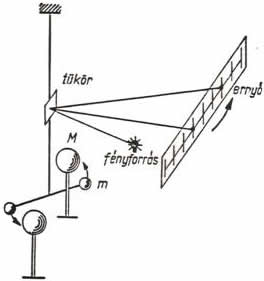
    • Cavendish torziós szálra egy tükröt és egy pálcát erősített, és arra szimmetrikusan két m tömegű testet.
    • Ezt követően r távolságra M tömegű testet helyezett el.
    • A gravitációs erő hatására a torziós szál elcsavarodott.
    • Az elcsavarodás szögét a torziós szálon lévő tükörre vetített fénysugár segítségével mérte meg.
    • Ebből kiszámolta a gravitációs erőt, és az M-et, m-et, r-t megmérte. Így meghatározható a gravitációs állandó.

  5. A gravitációs térerősség és potenciál
    A gravitációs mező jellemzésére szolgáló fizikai mennyiségek:
    1. gravitációs térerősség,
    2. gravitációs potenciál.
    1. A gravitációs térerősség

      A gravitációs mező erősségét jellemző vektormennyiség a gravitációs térerősség.

      Jele:

      A gravitációs mezőbe pontról pontra egységnyi tömegű próbatestet helyezünk.

      A próbatestre ható gravitációs erő és a próbatest tömegének hányadosa a mező adott pontjában állandó, és a mező erősségére jellemző vektormennyiség. Ez a gravitációs térerőség.

      Ha a gravitációs mezőt a M tömegű test hozza létre, akkor a gravitációs térerősség:

      A gravitációs térerősség egyenesen arányos a gravitációs mezőt létrehozó tömeggel és fordítottan arányos a mezőt létrehozó tömegtől mért távolság négyzetével. Az arányossági tényező a gravitációs állandó.

      Összefoglalva

      • A gravitációs térerősség vektormennyiség.
      • Nagysága:

        a gravitációs mezőbe helyezett próbatömegre ható gravitációs erő és a próbatest tömegének a hányadosa.

      • Iránya:

        a két tömeget összekötő egyenes mentén a mezőt létrehozó tömeg felé mutató vektor.

    2. Gravitációs potenciál

      A gravitációs potenciál munkavégzés szempontjából jellemzi a gravitációs mezőt.

      A gravitációs potenciál () olyan a gravitációs mező pontjaira jellemző skalármennyiség, amelyet a gravitációs mező ellenében végzünk, amíg az egységnyi tömegű próbatestet (gyorsítás nélkül) a nulla pontból a tetszőleges P pontba visszük.

      • M tömegű test gravitációs terében a tőle r távolságra lévő pont gravitációs potenciálja:

      • Ha nullpontként a Föld felszínét választjuk, akkor a potenciál nagysága:

  6. Gravitációval összekapcsolható jelenségek, fogalmak
    1. Eötvös-féle torziós inga

      A tömeg mérésére kétféle lehetőség adódik.

      1. Egy test gyorsítása során fellépő tehetetlenség mértékét tehetetlen tömeggel szokás jellemezni.
      2. A gravitációs kölcsönhatásban egy testet jellemző tömeget súlyos tömegnek nevezzük.

      Egy test tehetetlen és súlyos tömege megegyezik. Ezt először Eötvös Loránd bizonyította, az általa készítetett torziós ingával.

      A kísérlet azon alapul, hogy a Földön egy testre ható nehézségi erő (Fneh) két olyan erő eredője, amelyek közül az egyik a test súlyos tömegével arányos (gravitációs erő: Fg), a másik a test tehetetlen tömegével (centrifugális erő: Fcf)

      Ebből következik, hogy adott földrajzi helyen a nehézségi erő iránya a súlyos és a tehetetlen tömeg arányától függ.
      Eötvös Loránd egy nagyon érzékeny torziós mérleget készített, melynek rúdjait K-Ny irányba állította. A rúd egyik végére platina súlyt, a másik végére pontosan vele azonos tömegű, de más anyagi minőségű testet erősített.
      Ha a két testre a súlyos és a tehetetlen tömeg hányadosa más lenne, akkor a rúdra ható erők elcsavarnák a rudat.
      Eötvös különböző anyagi minőségű testeket hasonlított össze az etalonként használt platina súllyal, de egyetlen esetben sem tapasztalta a rúd elfordulását. Ezzel bizonyította, hogy a testek tehetetlen és súlyos tömege igen nagy pontossággal megegyezik.

      Eötvös-féle torziós inga nagyon precíz mérések elvégzésére alkalmas. Így segítségével kimutatható a Föld belsejében a sűrűség változása. Ez tette lehetővé, hogy felhasználják pl. kőolajmezők feltérképezésére.

    2. Súly

      A gravitációs mezőben a testeket erőhatás éri. Ha ezeket a testeket egy felfüggesztés vagy egy alátámasztás egyensúlyban tartja, akkor ezek a testek is erőhatást fejtenek ki a felfüggesztésükre vagy az alátámasztásukra.

      Az az erő, amely a gravitációs vonzás miatt húzza a felfüggesztést vagy nyomja a vízszintes alátámasztást a test súlya.

      Jele: G vagy Fg.
      Tehát a súlyerő mindig az alátámasztásra illetve a felfüggesztésre hat.

      A nyugalomban lévő test súlya és a testet érő gravitációs erő egyenlő nagyságú, de két különböző erő.
      • A súly,
      • a gravitációs vagy nehézségi erő,
      • és a testet tartó erő
      		 három különböző erő.
    3. Súlytalanság
      • Egy gravitációs mezőben lévő test akkor van súlytalansági állapotban, ha nincs alátámasztva vagy felfüggesztve, hiszen akkor nem fejt ki súlyt semmire.
      • Ilyenkor a rendszer elemei a gravitációs mező ellenére sem fejtenek ki egymásra kölcsönös nyomást.
      • Általánosan megfogalmazva: bármely rendszer a súlytalansági állapotba kerülhet, ha a gravitációs mező hatásán kívül semmilyen más külső erőhatás nem éri, és a rendszer haladó mozgást végez.
      • Ezek a feltételek megvalósulnak egy szabadon eső testen, vagy a Földünk mesterséges holdjain, illetve az űrhajókban, ha azok szabadon repülnek, azaz kikapcsolt hajtóművel haladnak.
    4. Bolygók mozgás

      A bolygók mozgását Kepler három törvénye írja le. Arra, hogy miért így mozognak Isaac Newton adott magyarázatot. Felismerte, hogy a bolygók és a Nap között gravitációs vonzás van, és ennek a vonzóerőnek az iránya a bolygót a Nappal összekötő egyenes irányába esik. Kimutatta, hogy az égitestek közötti gravitációs vonzóerő nagysága a gravitációs erőtörvénnyel számítható ki.

    5. Első és második kozmikus sebesség

      Az emberi tudás lehetővé tette, hogy a 20. század ötvenes éveitől kezdve mesterséges égitesteket juttassunk

      • a Föld köré,
      • a Nap köré és
      • a Naprendszeren kívülre.

      A mesterséges égitestek pályája és mozgása attól függ, hogy a Földön milyen magasra juttattuk fel, és ott milyen nagyságú és irányú sebességgel indítottuk el őket.

      Így elérhető, hogy

      • mesterséges holdként mozogjanak a Föld körül, vagy
      • mesterséges bolygóként a Nap körül, vagy
      • csillagközi szondaként elhagyják a Naprendszerünket.

      Első kozmikus sebesség

      Az első kozmikus sebesség az a sebesség, amellyel a Föld középpontjától r távolságra a Föld felszínével párhuzamosan el kell indítani egy testet, hogy Föld körüli pályán keringjen.

      Ez akkor valósul meg, ha a gravitációs erő biztosítja a körpályán maradáshoz szükséges centripetális erőt.


      I. kozmikus sebesség vagy körsebesség.

      Ha a testnek az érintő irányú sebessége ennél kisebb, akkor a test visszaesik a Földre.

      Második kozmikus sebesség

      A második kozmikus sebesség az a sebesség, amellyel, ha érintő irányban elindítják a mesterséges égitestet, akkor az kiszakad a Föld vonzásából.

      A gravitációs erő ellenében végzett munka, ha egy test végtelen távol kerül a Föld felszínétől:

      Ezt a munkát az indításkor kapott mozgási energia fedezi:

      Így:

      II. kozmikus sebesség vagy szökési sebesség.

    6. Csillagok életét meghatározó gravitáció
      • A csillagok élete a Világegyetemben kavargó hidrogénnel kezdődik. Ha a véletlenszerű mozgás következtében kialakul egy kb. 16 billió km átmérőjű hidrogénből álló gázfelhő, akkor abban már fellép akkora gravitációs vonzás, hogy nem engedi az atomokat szétrepülni.
      • A gravitációs vonzás következtében a részecskék gyorsulnak a centrum felé. Ez a mozgás idézi elő a csillag hőmérsékletének emelkedését, amely a magreakcióhoz vezet.
      • A magreakció beindulása után a kiáramló energia "felfújná" a csillagot, de a fellépő gravitációs vonzás biztosítja az egyensúlyt.